Vektor
Formel
Beschriftung im kartesischen Koordinatensystem
Die drei Koordinatenachsen stehen im kartesischen Koordinatensystem orthogonal (in 90°) aufeinander. Die Achsen werden entweder mit x,y und z beschriftet oder mit x1, x2, x3.
Punkt im \({{\Bbb R}^2},\,\,\,{{\Bbb R}^3}\)
Die Lage eines Punkts ist durch den Abstand je Koordinatenrichtung vom Ursprung des Koordinatensystems bestimmt. Abhängig davon, wie die Koordinatenachsen beschriftet wurdenm gibt es unterschiedliche Möglichkeiten Punkte und Vektoren zu beschriften
\(\begin{array}{l} {\Bbb R^{2:}}:P\left( {{P_x}\left| {{P_y}} \right.} \right) \buildrel \wedge \over = P\left( {{P_1}\left| {{P_2}} \right.} \right)\\ {\Bbb R^3}:P\left( {{P_x}\left| {{P_y}\left| {{P_z}} \right.} \right.} \right) \buildrel \wedge \over = P\left( {{P_1}\left| {{P_2}\left| {{P_3}} \right.} \right.} \right) \end{array}\)
Skalar
Skalar ist ein Ausdruck in der Vektorrechnung für eine relle Zahl. Man verwendet den Begriff Skalar um die Richtungsunabhängigkeit einer Größe im Unterschied zum richtungsabhängigen Vektor zu betonen.
Vektor
Ein Vektor ist eine Strecke in der Ebene oder im Raum. Jeder Vektor ist durch Richtung, Orientierung und durch Betrag gekennzeichnet. Vektoren können im Raum beliebig parallelverschoben werden, d.h. ihr Anfangspunkt kann beliebig festgelegt werden, daraus ergibt sich dann ein eindeutiger Endpunkt. Vektoren spielen in der Physik eine große Rolle, so ist etwa die Geschwindigkeit kein Skalar, sondern ein Vektor.
- Geometrisch wird ein Vektor durch einen Pfeil, mit einem Schaft und einer Spitze (definiert die Orientierung) repräsentiert.
- Algebraisch sind Vektoren eindimensionale Listen von Zahlen, wobei die Komponenten des Vektors in Form von Zeilen- und als Spaltenvektor angeschrieben werden können. Die Anzahl der Komponenten eines Vektors stimmt mit der Dimension des Vektors überein. (ax,ay,az) repräsentiert also einen 3-dimensionalen Vektor. Die Reihenfolge in der die Komponenten angeschrieben werden spielt eine wesentliche Rolle dabei, in welche Richtung der Vektor zeigt
\(\eqalign{ & \overrightarrow a = \overrightarrow {{a_x}} + \overrightarrow {{a_y}} + \overrightarrow {{a_z}} = \left( {\matrix{ {{a_x}} \cr {{a_y}} \cr {{a_z}} \cr } } \right) \cr & \overrightarrow a = {a_x} \cdot \overrightarrow i + {a_y} \cdot \overrightarrow j + {a_z} \cdot \overrightarrow k \cr}\)
Illustration eines Vektors vom Ursprung zum Punkt P
Gegenvektor
Den Gegenvektor erhält man, indem man den Ausgangsvektor um 180° dreht, bzw. indem man den Ausgangsvektor mit dem Skalar -1 multipliziert. Vektor und Gegenvektor haben den gleichen Betrag, die gleiche Richtung aber entgegengesetzte Orientierung.
\(\overrightarrow a = \left( {\begin{array}{*{20}{c}}
{{a_x}}\\
{{a_y}}\\
{{a_z}}
\end{array}} \right) \Leftrightarrow - \overrightarrow a = - 1 \circ \overrightarrow a = \left( {\begin{array}{*{20}{c}}
{ - {a_x}}\\
{ - {a_y}}\\
{ - {a_z}}
\end{array}} \right)\)
Betrag eines Vektors
Der Betrag bzw. die Länge des Vektors ergeben sich aus dem Abstand zwischen seinem Anfangspunkt, dem Schaft im Punkt "P" und seinem Endpunkt, also seiner Spitze in "Q".
\(\left| {\overrightarrow {PQ} } \right| = \left| {\overrightarrow v } \right| = \sqrt {{{\left( {{Q_x} - {P_x}} \right)}^2} + {{\left( {{Q_y} - {P_y}} \right)}^2} + {{\left( {{Q_z} - {P_z}} \right)}^2}} = \sqrt {{v_x}^2 + {v_y}^2 + {v_z}^2} \)
\(\left| {\overrightarrow v } \right| = \left| {\left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right)} \right| = \sqrt {{v_x}^2 + {v_y}^2 + {v_z}^2} \)
Illustration zur Richtung und zur Berechnung vom Betrag eines zweidimensionalen Vektors
Richtung des Vektors
Die Richtung eins Vektors ist durch seine Lage relativ zu den Achsen des Koordinatensystems bestimmt. Ein Vektor hat eine einzige Richtung! Die Richtung des Vektors kann man aus dem Arkustangens vom Quotienten aus der Differenz der y-Koordinaten und der Differenz der x-Koordinaten zweier Punkte vom Vektor berechnen.
\(\alpha = \arctan \dfrac{{{Q_y} - {P_y}}}{{{Q_x} - {P_x}}}\)
Orientierung eines Vektors
Vektoren mit gleicher Richtung haben entweder gleiche oder entgegengesetzte Orientierung. Die Orientierung wird durch Schaft und Spitze des Vektors definiert. Ein Gegenvektor ist ein Vektor mit gleichem Betrag und gleicher Richtung aber umgekehrter Orientierung als der betrachtete Vektor.
Gleiche Vektoren
Vektoren sind gleich, wenn sie gleich lang, parallel und gleich orientiert (Pfeilspitze) sind. Gleiche Vektoren können unterschiedliche Koordinatendarstellungen haben.
Illustration zur Orientierung, zur Gleichheit von Vektoren und zum Gegenvektor eines Vektors und zu Vektoren mit gleichem Betrag
Nullvektor
Der Nullvektor \(\overrightarrow 0\) hat keine bestimmte Richtung. Seine Länge (sein Betrag) ist null. Der Nullvektor ist das neutrale Element bezüglich der Addition von Vektoren. Schaft und Spitze vom Nullvektor fallen in einem Punkt zusammen.
\(\begin{array}{l} \overrightarrow 0 = \left( {0\left| 0 \right.} \right) = \left( {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right)\\ \overrightarrow {AA} = 0 \end{array}\)
Der Nullvektor ist kollinear zu jedem anderen Vektor und komplanar zu einer von 2 Vektoren aufgespannten Ebene.
Basisvektor
Die Basisvektoren liegen jeweils in einer Koordinatenachse, ihre Länge d.h. ihr Betrag ist 1. Sie spannen das Koordinatensystem auf. Je Dimension gibt es einen eigenen Basisvektor. Seine Komponenten bestehen aus einer "1" und sonst nur aus Nullen.
\(\eqalign{ & \overrightarrow i = \left( {\matrix{ 1 \cr 0 \cr } } \right) \cr & \overrightarrow j = \left( {\matrix{ 0 \cr 1 \cr } } \right) \cr}\)
Einheitsvektor
Der Einheitsvektor \( \overrightarrow {{r_0}}\), hat dieselbe Richtung wie der Richtungs- bzw. der Ortsvektor \( \overrightarrow r\), seine Länge wurde aber auf 1 normiert.
\(\eqalign{ & \overrightarrow {{r_0}} = {{\overrightarrow r } \over {\left| r \right|}} = \left( {\matrix{ {{{{r_x}} \over {\sqrt {{{\left( {{r_x}} \right)}^2} + {{\left( {{r_y}} \right)}^2}} }}} \cr {{{{a_y}} \over {\sqrt {{{\left( {{r_x}} \right)}^2} + {{\left( {{r_y}} \right)}^2}} }}} \cr } } \right) \cr & {\rm{mit}}\,\,\,\left| {\overrightarrow r } \right| \ne 0 \cr}\)
Ortsvektor
Der Ortsvektor ist der Vektor vom Ursprung des Koordinatensystems zu einem gegebenen Punkt. Ein Ortsvektor \(\overrightarrow a\) hat seinen Anfang immer im Ursprung des Koordinatensystems. Seine Richtung, Orientierung und Betrag ergeben sich aus der Lage seines Endpunkts. Einen Ortsvektor darf man daher nicht parallel verschieben, man darf auch nicht seinen Betrag ändern.
\(\overrightarrow a = x.\overrightarrow i + y.\overrightarrow j = \left( {\matrix{ x \cr y \cr } } \right) = \left( {x,y} \right)\)
Verbindungsvektor
Der Verbindungsvektor verbindet zwei Punkte im Raum. Es sind die Punkte P (Px l Py) und Q (Qx l Qy) gegeben. Der Verbindungsvektor ist jener Vektor, der in P seinen Schaft und in Q seine Spitze hat. Um ihn zu berechnen subtrahiert man vom Ortsvektor zu Q (Spitze) den Ortsvektor zu P (Schaft). Einen Verbindungsvektor darf man daher nicht parallel verschieben, man darf auch nicht seinen Betrag oder seine Orientierung ändern.
In \({{\Bbb R}^2}\):
\(\overrightarrow v = \overrightarrow {PQ} = \overrightarrow {UQ} - \overrightarrow {UP} = Q - P = \left( {\begin{array}{*{20}{c}} {{Q_x} - {P_x}}\\ {{Q_y} - {P_y}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}} \end{array}} \right)\)
In \({{\Bbb R}^3}\):
\(\begin{array}{l} A\left( {{A_x}\left| {{A_y}\left| {{A_z}} \right.} \right.} \right)\\ B\left( {{B_x}\left| {{B_y}\left| {{B_z}} \right.} \right.} \right)\\ \overrightarrow {AB} = B - A = \left( {\begin{array}{*{20}{c}} {{B_x} - {A_x}}\\ {{B_y} - {A_y}}\\ {{B_z} - {A_z}} \end{array}} \right) \end{array}\)
"Spitze minus Schaft Regel": Man erhält den Verbindungsvektor zweier Punkte, indem man Komponentenweise die Koordinaten von der Spitze minus jener vom Schaft anschreibt.
Illustration vom Verbindungsvektor zwischen 2 Punkten
Richtungsvektor als Parallelvektor zum Verbindungsvektor
Der Richtungsvektor \(\overrightarrow r\) ist entweder der Verbindungsvektor oder ein zum Verbindungsvektor paralleler Vektor. Der Richtungsvektor hat zwar eine definierte Länge, aber keine feste Position im Koordinatensystem d.h. er kann parallel verschoben werden und ist noch immer ein Richtungsvektor. Der Verbindungsvektor ist ein besonderer Richtungsvektor, weil sein Anfangs- bzw. Endpunkt mit den besonderen Punkten P und Q zusammenfallen.
Mehrdimensionaler Vektor
Die Anzahl der Komponenten eines Vektors entspricht der Dimension des Raums. Dreidimensionale Vektoren spannen den uns vertrauten dreidimensionalen Raum aus Breite, Tiefe und Höhe auf. Vierdimensionale Vektoren spannen die Raum-Zeit der Physik auf. Bei höherdimensionalen Vektoren nummeriert man die Komponenten, weil die Dimensionen mitunter keinen anschaulichen Namen haben.
\(\eqalign{ & P = \left( {{P_1}\left| {{P_2}\left| {...\left| {{P_n}} \right.} \right.} \right.} \right) \cr & Q = \left( {{Q_1}\left| {{Q_2}\left| {...\left| {{Q_n}} \right.} \right.} \right.} \right) \cr}\)
n-dimensionaler Richtungsvektor von P nach Q:
\(\overrightarrow {PQ} = \left( {\begin{array}{*{20}{c}} {{Q_1} - {P_1}}\\ {{Q_2} - {P_2}}\\ {...}\\ {{Q_n} - {P_n}} \end{array}} \right)\)
Schon den nächsten Badeurlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Damit niemand mehr bei Mathe in's Schwimmen kommt!

Wissenspfad
Zur aktuellen Lerneinheit empfohlenes Vorwissen
| Geometrie | Wissenswertes über: Geometrie ebener Figuren und von Körpern, Trigonometrie - Winkelfunktionen, Vektorrechnung in der Ebene und im Raum, Analytische lineare Geometrie: Punkt, Gerade und Ebene, 2 und 3-dimensional, Analytische nichtlineare Geometrie: Kreis und Kugel, Analytische nichtlineare Geometrie: Kegelschnitte und Raumkurven |
Aktuelle Lerneinheit
| Vektor | Ein Vektor ist durch seine Richtung, seine Orientierung und durch seinen Betrag gekennzeichnet |
Verbreitere dein Wissen zur aktuellen Lerneinheit
| Geometrische Grundbegriffe von Figuren und Körpern | Die geometrischen Grundbegriffe eröffnen den Einstig in die Geometrie, und definieren deren grundlegende Elemente |
| Abbildungsgeometrie | In der Abbildungsgeometrie unterscheidet man zwischen Kongruenzabbildungen und Ähnlichkeitsabbildungen |
| Analytische Geometrie | Bei der analytischen Geometrie werden Aufgaben der Geometrie auf Aufgaben der Algebra zurückgeführt |
| Trigonometrie | Es geht bei der Trigonometrie um die Berechnung von rechtwinkeligen Dreiecken mit Hilfe vom Verhältnis zweier Dreiecksseiten |
| Koordinatensysteme | Koordinatensysteme dienen dazu, die gegenseitige Beziehung von Punkten zueinander und zum Ursprung des Koordinatensystems in zweckmäßig vielen Dimensionen anzugeben |
Vertiefe dein Wissen zur aktuellen Lerneinheit
| Vektoralgebra | Die Vektoralgebra beschäftigt sich mit den Grundrechenregeln für Vektoren |
| Vektoranalysis |
Bild
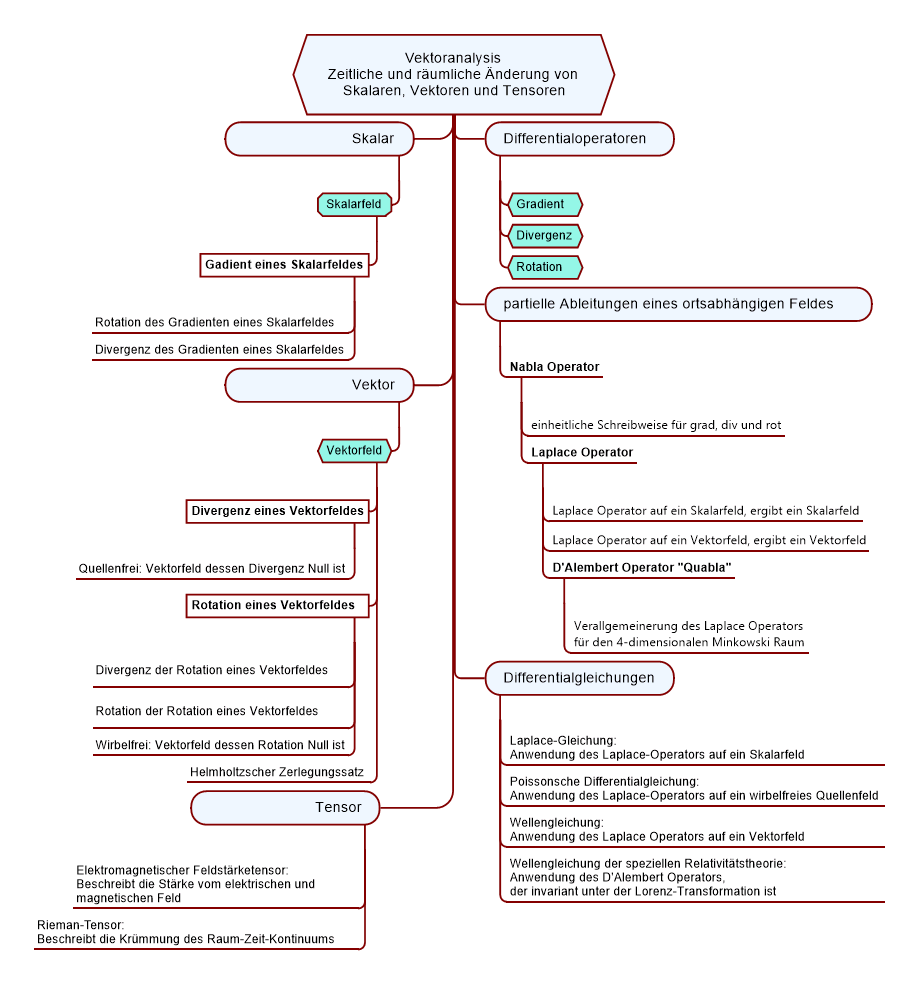 |
| Multiplikation von Vektoren | Bei der Multiplikation von Vektoren unterscheidet man zwischen 1) der Multiplikation eines Vektors mit einem Skalar, 2) dem Skalarprodukt und 3) dem Vektorprodukt. Die Namen weisen bereits darauf hin, beim Skalarprodukt ist das Resultat ein Skalar - also eine reelle Zahl, während beim Vektorprodukt das Resultat ein Vektor ist. |
| Geometrische Operationen mittels Vektorrechnung | Von einem Anfangspunkt aus soll ein Vektor gezeichnet werden. Gesucht sind die Koordinaten vom Endpunkt des Vektors. |
Aufgaben zu diesem Thema
Aufgabe 84
Vektoren in der Physik
Erkläre an Hand zweier Beispiele aus der Physik, was einen Vektor ausmacht.
Aufgabe 4040
p>Standardisierte kompetenzorientierte schriftliche Reifeprüfung Angewandte Mathematik
Quelle: BHS Matura vom 10. Mai 2017 - Teil-B Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Kräfte - Aufgabe B_406
Teil a
Durch eine Kraft \({\overrightarrow F _{Zug}} = \left( {\begin{array}{*{20}{c}} {260}\\ {140} \end{array}} \right)\) Newton (N) wird eine Last von A nach B und danach von B nach C gezogen (siehe nachstehende Skizze).
1. Teilaufgabe - Bearbeitungszeit 11:20
Berechnen Sie die durch die Kraft FZug an der Last verrichtete Arbeit.
[2 Punkte]
Aufgabe 84
Vektoren in der Physik
Erkläre an Hand zweier Beispiele aus der Physik, was einen Vektor ausmacht.
Aufgabe 6013
Abitur 2015 Gymnasium Bayern - Prüfungsteil A - Geometrie
Angabe mit freundlicher Genehmigung vom Bayerischen Staatsministerium für Bildung und Kultus, Wissenschaft und Kunst
Die Gerade g verläuft durch die Punkte A(0 |1| 2) und B(2 | 5 | 6).
1. Teilaufgabe a.1) 1 BE - Bearbeitungszeit: 2:20
Zeigen Sie, dass die Punkte A und B den Abstand 6 haben.
Die Punkte C und D liegen auf g und haben von A jeweils den Abstand 12.
2. Teilaufgabe a.2) 2 BE - Bearbeitungszeit: 4:40
Bestimmen Sie die Koordinaten von C und D.
Die Punkte A, B und E(1| 2 | 5) sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden.
3. Teilaufgabe b) 2 BE - Bearbeitungszeit: 4:40
Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten. Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.
Schon den nächsten Urlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen.

Aufgabe 6029
Abitur 2015 Gymnasium Bayern - Prüfungsteil B - Geometrie
Angabe mit freundlicher Genehmigung vom Bayerischen Staatsministerium für Bildung und Kultus, Wissenschaft und Kunst
In einem kartesischen Koordinatensystem sind
- die Ebene \(E:{x_1} + {x_3} = 2\)
- der Punkt \(A\left( {0\left| {\sqrt 2 \left| 2 \right.} \right.} \right)\)
- und die Gerade \(g:\overrightarrow X = \overrightarrow A + \lambda \cdot \left( {\begin{array}{*{20}{c}} { - 1}\\ {\sqrt 2 }\\ 1 \end{array}} \right),\,\,\,\lambda \in {\Bbb R }\)
gegeben.
1. Teilaufgabe a.1) 1 BE - Bearbeitungszeit: 2:20
Beschreiben Sie, welche besondere Lage die Ebene E im Koordinatensystem hat.
2. Teilaufgabe a.2) 1 BE - Bearbeitungszeit 2:20
Weisen Sie nach, dass die Ebene E die Gerade g enthält.
3. Teilaufgabe a.3) 2 BE - Bearbeitungszeit: 4:40
Geben Sie die Koordinaten der Schnittpunkte von E mit der x1-Achse und mit der x3 -Achse an.
4. Teilaufgabe a.4) 2 BE - Bearbeitungszeit: 4:40
Veranschaulichen Sie die Lage der Ebene E sowie den Verlauf der Geraden g in einem kartesischen Koordinatensystem (vgl. Abbildung).
Die x1x2-Ebene beschreibt modellhaft eine horizontale Fläche, auf der eine Achterbahn errichtet wurde. Ein gerader Abschnitt der Bahn beginnt im Modell im Punkt A und verläuft entlang der Geraden g. Der Vektor
\(\overrightarrow v = \left( {\begin{array}{*{20}{c}} { - 1}\\ {\sqrt 2 }\\ 1 \end{array}} \right)\)
beschreibt die Fahrtrichtung auf diesem Abschnitt.
5. Teilaufgabe b.1) 3 BE - Bearbeitungszeit: 7:00
Berechnen Sie im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt.
6. Teilaufgabe b.2) 2 BE - Bearbeitungszeit: 4:40
Berechnen Sie im Modell die zugehörige Steigung dieses Abschnitts in Prozent.
An den betrachteten geraden Abschnitt der Achterbahn schließt sich – in Fahrtrichtung gesehen – eine Rechtskurve an, die im Modell durch einen Viertelkreis beschrieben wird, der in der Ebene E verläuft und den Mittelpunkt \(M\left( {0\left| {3 \cdot \sqrt 2 \left| 2 \right.} \right.} \right)\) hat. Das Lot von M auf g schneidet g im Punkt B. Im Modell stellt B den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt.
7. Teilaufgabe c.1) 2 BE - Bearbeitungszeit: 4:40
Bestimmen Sie die Koordinaten von B.
8. Teilaufgabe c.2) 3 BE - Bearbeitungszeit: 7:00
Berechnen Sie den Kurvenradius im Modell.
(Teilergebnis: \(B\left( { - 1\left| {2 \cdot \sqrt 2 \left| 3 \right.} \right.} \right)\)
Das Ende der Rechtskurve wird im Koordinatensystem durch den Punkt C beschrieben.
9. Teilaufgabe d) 2 BE - Bearbeitungszeit: 4:40
Begründen Sie, dass für den Ortsvektor des Punkts C gilt: \(\overrightarrow C = \overrightarrow M + \overrightarrow v \)
Ein Wagen der Achterbahn durchfährt den Abschnitt, der im Modell durch die Strecke [AB] und den Viertelkreis von B nach C dargestellt wird, mit einer durchschnittlichen Geschwindigkeit von 15 m/s.
10. Teilaufgabe e) 4 BE - Bearbeitungszeit: 9:20
Berechnen Sie die Zeit, die der Wagen dafür benötigt, auf Zehntelsekunden genau, wenn eine Längeneinheit im Koordinatensystem 10 m in der Realität entspricht.
Aufgabe 6014
Abitur 2015 Gymnasium Bayern - Prüfungsteil A - Geometrie
Angabe mit freundlicher Genehmigung vom Bayerischen Staatsministerium für Bildung und Kultus, Wissenschaft und Kunst
Betrachtet wird die Pyramide ABCDS mit A(0 | 0 | 0), B(4 | 4 | 2) , C(8 | 0 | 2), D(4 | -4 | 0) und S(1|1| -4) . Die Grundfläche ABCD ist ein Parallelogramm.
Teilaufgabe a) 2 BE - Bearbeitungszeit: 4:40
Weisen Sie nach, dass das Parallelogramm ABCD ein Rechteck ist.
Die Kante \(\left[ {AS} \right]\) senkrecht auf der Grundfläche ABCD. Der Flächeninhalt der Grundfläche beträgt \(24 \cdot \sqrt 2 \)
Teilaufgabe b) 3 BE - Bearbeitungszeit: 7:00
Ermitteln Sie das Volumen der Pyramide.
Aufgabe 6030
Abitur 2015 Gymnasium Bayern - Prüfungsteil B - Geometrie
Angabe mit freundlicher Genehmigung vom Bayerischen Staatsministerium für Bildung und Kultus, Wissenschaft und Kunst
Die Abbildung zeigt eine Sonnenuhr mit einer gegenüber der Horizontalen geneigten, rechteckigen Grundplatte, auf der sich ein kreisförmiges Zifferblatt befindet. Auf der Grundplatte ist der Polstab befestigt, dessen Schatten bei Sonneneinstrahlung die Uhrzeit auf dem
Zifferblatt anzeigt. Eine Sonnenuhr dieser Bauart wird in einem kartesischen Koordinatensystem modellhaft dargestellt (siehe nachfolgende Abbildung).
Dabei beschreibt das Rechteck ABCD mit \(A\left( {5\left| { - 4\left| 0 \right.} \right.} \right)\) und \(B\left( {5\left| {4\left| 0 \right.} \right.} \right)\) die Grundplatte der Sonnenuhr. Der Befestigungspunkt des Polstabs auf der Grundplatte wird im Modell durch den Diagonalenschnittpunkt \(M\left( {2,5\left| {0\left| 2 \right.} \right.} \right)\) des Rechtecks ABCD dargestellt. Eine Längeneinheit im Koordinatensystem entspricht 10cm in der Realität. Die Horizontale wird im Modell durch die x1x2-Ebene beschrieben.
1. Teilaufgabe a.1) 2 BE - Bearbeitungszeit: 4:40
Bestimmen Sie die Koordinaten des Punkts C.
2. Teilaufgabe a.2) 3 BE - Bearbeitungszeit: 7:00
Ermitteln Sie eine Gleichung der Ebene E, in der das Rechteck ABCD liegt, in Normalenform.
(mögliches Teilergebnis: \(E:4{x_1} + 5{x_3} - 20 = 0\))
Die Grundplatte ist gegenüber der Horizontalen um den Winkel α geneigt. Damit man mit der Sonnenuhr die Uhrzeit korrekt bestimmen kann, muss für den Breitengrad φ des Aufstellungsorts der Sonnenuhr \(\alpha + \varphi = 90^\circ \) gelten.
3. Teilaufgabe b) 4 BE - Bearbeitungszeit: 9:20
Bestimmen Sie, für welchen Breitengrad φ die Sonnenuhr gebaut wurde.
Der Polstab wird im Modell durch die Strecke \(\left[ {MS} \right]{\rm{ mit }}S\left( {4,5\left| {0\left| {4,5} \right.} \right.} \right)\) dargestellt.
4. Teilaufgabe c.1) 1 BE - Bearbeitungszeit: 2:20
Zeigen Sie, dass der Polstab senkrecht auf der Grundplatte steht.
5. Teilaufgabe c.2) 2 BE - Bearbeitungszeit: 4:40
Berechnen Sie die Länge des Polstabs auf Zentimeter genau.
Sonnenlicht, das an einem Sommertag zu einem bestimmten Zeitpunkt t0 auf die Sonnenuhr einfällt, wird im Modell durch parallele Geraden mit dem Richtungsvektor
\(\overrightarrow u = \left( {\begin{array}{*{20}{c}} 6\\ 6\\ { - 13} \end{array}} \right)\)dargestellt.
6. Teilaufgabe d) 6 BE - Bearbeitungszeit: 14:00
Weisen Sie nach, dass der Schatten der im Modell durch den Punkt S dargestellten Spitze des Polstabs außerhalb der rechteckigen Grundplatte liegt.
Um 6 Uhr verläuft der Schatten des Polstabs im Modell durch den Mittelpunkt der Kante \(\left[ {BC} \right]\), um 12 Uhr durch den Mittelpunkt der Kante \(\left[ {AB} \right]\) und um 18 Uhr durch den Mittelpunkt der Kante \(\left[ {AD} \right]\).
7. Teilaufgabe e) 2 BE - Bearbeitungszeit: 4:40
Begründen Sie, dass der (in Teilaufgabe c, Anm.) betrachtete Zeitpunkt t0 vor 12 Uhr liegt.
Im Verlauf des Vormittags überstreicht der Schatten des Polstabs auf der Grundplatte in gleichen Zeiten gleich große Winkel.
8. Teilaufgabe f) 3 BE - Bearbeitungszeit: 7:00
Bestimmen Sie die Uhrzeit auf Minuten genau, zu der der Schatten des Polstabs im Modell durch den Punkt B verläuft.
Aufgabe 104
Verbindungsvektor
Es sind folgende 2 Punkte gegeben:
\(P\left( {\matrix{ {15} \cr { - 2} \cr 2 \cr } } \right);\,\,\,\,\,Q\left( {\matrix{ 3 \cr 2 \cr 5 \cr } } \right);\)
1. Teilaufgabe: Berechne die Koordinaten des Verbindungsvektors: \(\overrightarrow v = \overrightarrow {PQ}\)
2. Teilaufgabe: Berechne den Betrag des Verbindungsvektors: \(\left| {\overrightarrow v } \right|\)
Schon den nächsten Urlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen.

Aufgabe 108
Parallelogramm mittels Vektoren berechnen
Gegeben ist ein Parallelogramm mit:
\(A\left( {\begin{array}{*{20}{c}} 2\\ { - 2} \end{array}} \right);\,\,\,\,\,B\left( {\begin{array}{*{20}{c}} 3\\ 1 \end{array}} \right);\,\,\,\,\,C\left( {\begin{array}{*{20}{c}} { - 4}\\ 3 \end{array}} \right);\)
1. Teilaufgabe: Prüfe, ob es sich tatsächlich „nur“ um ein Parallelogramm handelt, oder ob nicht sogar ein Rechteck vorliegt
2. Teilaufgabe: Berechne die Koordinaten von D auf 2 Arten
3. Teilaufgabe: Berechne den Umfang der Figur
Aufgabe 4057
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Angewandte Mathematik
Quelle: BHS Matura vom 10. Mai 2017 - Teil-B Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Straßenbau - Aufgabe B_408
Teil b
Zwischen zwei Punkten C und D soll eine geradlinige Verbindungsstraße errichtet werden (siehe nachstehendes Koordinatensystem).
1. Teilaufgabe - Bearbeitungszeit 5:40
Ermitteln Sie die Koordinaten des Vektors \(\overrightarrow {CD} \)
[1 Punkt]
2. Teilaufgabe - Bearbeitungszeit 5:40
Berechnen Sie den Betrag des Vektors \(\overrightarrow {CD} \)
[1 Punkt]
Aufgabe 4331
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Angewandte Mathematik
Quelle: BHS Matura vom 08. Mai 2019 - Teil-B Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
Boule - Aufgabe B_444
Boule ist eine Sportart, bei der Kugeln geworfen werden. Ziel ist es, mit den eigenen Kugeln möglichst nah an eine Zielkugel zu gelangen.
Teil b
Für eine genauere Analyse eines Boule-Spiels wird mithilfe einer Drohne ein Luftbild aufgenommen.
- A = (2 | 10) ... Auflagepunkt der ersten Kugel
- B = (17 | 6) ... Auflagepunkt der zweiten Kugel
- Z = (4 | 1) ... Auflagepunkt der Zielkugel
1. Teilaufgabe - Bearbeitungszeit 5:40
Berechnen Sie die Lange der Strecke BZ.
[1 Punkt]
Während des Spiels bewegt sich die erste Kugel entlang der Strecke AB 3 cm in Richtung B.
2. Teilaufgabe - Bearbeitungszeit 11:20
Berechnen Sie die Koordinaten der neuen Position des Auflagepunkts der ersten Kugel.
[2 Punkte]
Aufgabe 4395
Standardisierte kompetenzorientierte schriftliche Reifeprüfung Angewandte Mathematik
Quelle: BHS Matura vom 28. Mai 2020 - Teil-B Aufgabe
Angabe mit freundlicher Genehmigung vom Bundesministerium für Bildung; Lösungsweg: Maths2Mind
W-LAN - Aufgabe B_475
In einer Fabrikshalle wird mit Access-Points und Repeatern ein W-LAN eingerichtet. Ein Access-Point verbindet einen Laptop kabellos mit einem Netzwerk. Ein Repeater verstärkt das Signal. Die Datenübertragungsrate beschreibt die übertragene Datenmenge pro Zeiteinheit und wird meist in der Einheit Megabit pro Sekunde (Mbit/s) angegeben.
Teil c
Im Rahmen einer Testinstallation werden in der Fabrikshalle ein Access-Point, ein Repeater und 2 Laptops auf gleich hohe Tische gestellt (siehe nachstehende schematische Abbildung, Ansicht von oben).
Im Punkt A = (30 | 0) befindet sich der Access-Point. Die Laptops in den Punkten P1 = (20 | 2) und P2 = (45 | 20) sollen diesen Access-Point nutzen können.
1. Teilaufgabe - Bearbeitungszeit 5:40
Zeigen Sie mithilfe der Vektorrechnung, dass der Winkel α kleiner als 120° ist.
[1 Punkt]
2. Teilaufgabe - Bearbeitungszeit 5:40
Zeichnen Sie in der obigen Abbildung denjenigen Punkt P3 ein, der folgendermaßen bestimmt werden kann:
\(\overrightarrow {O{P_3}} = \overrightarrow {O{P_2}} - \dfrac{1}{3} \cdot \overrightarrow {{P_1}{P_2}} \)
1 Punkt]
Ein Repeater soll im Punkt R = (xR | 30) in einem Abstand von 40 m vom Access-Point im Punkt A montiert werden (siehe obige Abbildung).
3. Teilaufgabe - Bearbeitungszeit 5:40
Berechnen Sie xR.
[1 Punkt]
Schon den nächsten Urlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Nach der Prüfung mit dem gesparten Geld deinen Erfolg genießen.
