Logarithmieren

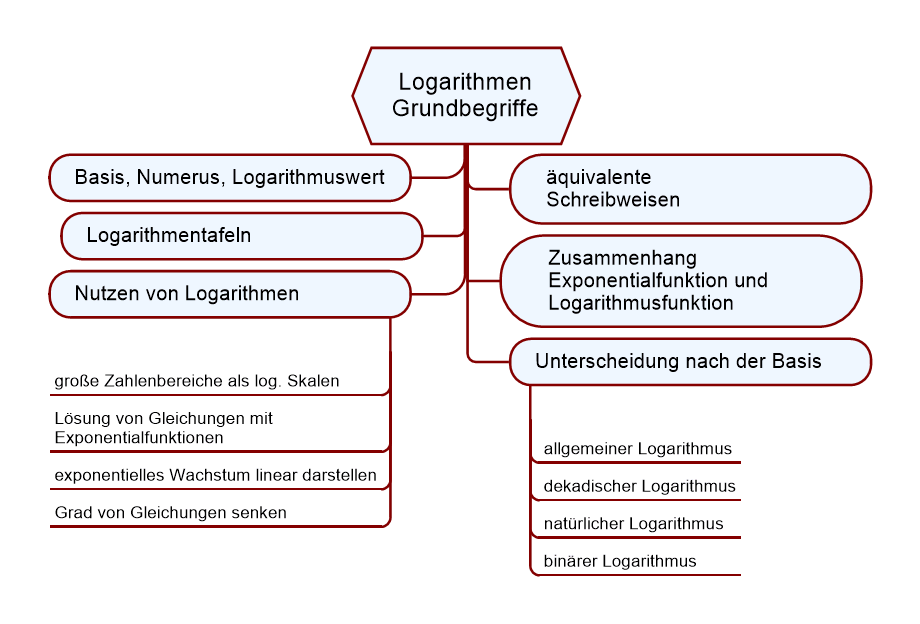
Logarithmieren

Logarithmieren ermöglicht es, x zu errechnen, wenn x Exponent einer Potenz ist.

\({a^x} = b \Leftrightarrow x = {\log _a}\left( b \right){ = ^a}\log b\)

Beispiel: Berechne x
\(\eqalign{ & {5^x} = 125 \cr & x = {}^5\log 125 \cr}\)

Bezeichnungen beim Logarithmieren

Ein Logarithmus wird durch seine Basis und seinen Numerus bestimmt. Für die Basis sind 10, die eulersche Zahl e und 2 üblich.

Es werden 2 äquivalente Schreibweisen für Logarithmen verwendet

\({}^a\log \,\,b = {\log _a}\,\,b\)

Unterscheidung von Logarithmen nach der Basis

Es ist möglich die Basis vom Logarithmus frei zu wählen, üblich ist es aber für die Basis entweder 10, die Eulersche Zahl e oder 2 zu wählen

Logarithmus von b zur Basis a​

Der Logarithmus von b zur Basis a ist jener Exponent, mit dem man a potenzieren muss, um b zu erhalten.

\(\eqalign{ & {}^a\log b = x \Leftrightarrow {a^x} = b \cr & a \in {{\Bbb R}^ + }\backslash \left\{ 1 \right\};\,\,b \in {{\Bbb R}^ + }\, \cr}\)

Den Zahlenwert von einem Logarithmus mit beliebiger Basis kann man berechnen, indem man den Logarithmus vom Numerus b durch den Logarithmus der Basis a dividiert

\(lo{b_b}\left( a \right) \buildrel \wedge \over = {}^a{\mathop{\rm logb}\nolimits} \) ist die eindeutige Lösung der Gleichung \({b^x} = a\) . Ihren Zahlenwert kann man berechnen indem man den Logarithmus vom Numerus b durch den Logarithmus der Basis a dividiert

\({}^a\log b = \dfrac{{\ln b}}{{\ln a}} = \dfrac{{\log b}}{{\log a}}\)

Beispiel:

\({}^2\log16 = x;\)

... folgende Umrechnung vereinfacht die Berechnung, sollte man keinen modernen Taschenrechner zur Hand haben:

\(x = \dfrac{{\ln 16}}{{\ln 2}} = \dfrac{{\log 16}}{{\log 2}} = 4\)

Natürlicher Logarithmus

Der natürliche Logarithmus hat die EULER‘sche Zahl e=2,71828 als Basis. Der Logarithmus naturalis ln(x) ist die Umkehrfunktion der Eulerschen Funktion e^x.

\(\eqalign{
& {D_f} = {{\Bbb R}^ + }\,\,\,\,\,{W_f} = {\Bbb R} \cr
& \ln (0)....{\text{ nicht definiert}} \cr
& {\text{ln}}\left( 1 \right) = 0 \cr} \)

\({\text{Basis = e: }}{}^e\log b = \ln b\)

Bild

Dekadischer Logarithmus

Der dekadische Logarithmus hat die Zahl 10 als Basis.

\({\text{Basis = 10: }}{}^{10}\log b = \lg b\)

Es ist zweckmäßig für die Basis b=10 zu wählen, denn dann kann man Logarithmen mit beliebiger Basis leicht berechnen.

\({}^b\log x = {}^a\log x \cdot {}^b\log a\,\, \Leftrightarrow \,\,{}^a\log x = \dfrac{{{}^b\log x}}{{{}^b\log a}}\)

Zusammenhang dekadischer Logarithmus und natürlicher Logarithmus

Bei der Umrechnung vom dekadischen auf den natürlichen Logarithmus erfolgt ein Wechsel der Basis von 10 auf e=2,718

\({}^a\log x = \dfrac{{\ln x}}{{\ln a}}\)

Binärer Logarithmus

Der binäre Logarithmus hat die Zahl 2 als Basis.

\({\text{Basis = 2: }}{}^2\log b = \operatorname{lb} b\)

Logarithmische Skala

Logarithmische Skalen werden verwendet, wenn der Wertebereich der darzustellenden Größe viele Zehnerpotenzen umfasst. Auf einer logarithmischen Skala werden Werte, die sich in gleichen Zeiträumen verzehnfachen als Gerade dargestellt. Kleine Werte sind genauer ablesbar als große Werte.

Bild

Dabei ergibt 10 hoch dem dekadischen Wert den entsprechenden logarithmischen Wert.

\(\begin{gathered} {10^0} = 1 \hfill \\ {10^1} = 10 \hfill \\ {10^2} = 100 \hfill \\ ... \hfill \\ {10^7} = 10.000.000 \hfill \\ \end{gathered} \)

Beispiele für logarithmische Skalen:

• Das Spektrum elektromagnetischer Wellen reicht von 10⁰ Hz bis 10²³ Hz. 
• Aktienkurse, die alle10 Jahre ihren Wert verzehnfachen, haben einen linear verlaufenden Graph, wenn die Zeitachse linear und die Werteachse logarithmisch beschriftet ist.
• Potenzfunktionen werden als Gerade dargestellt, wenn sowohl die x- als auch die y-Achse logarithmisch beschriftet sind.

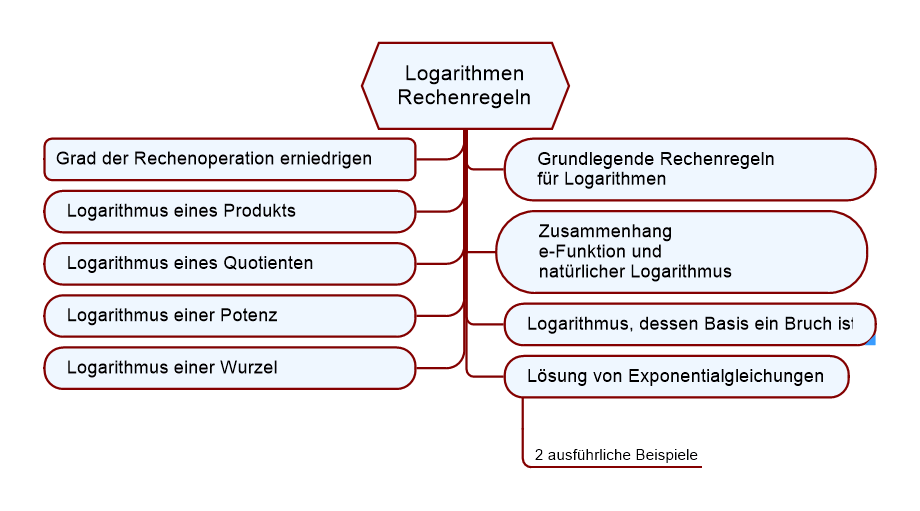
Rechenregeln für Logarithmen

Die Rechenregeln für Logarithmen erlauben es, den "Grad einer Rechenoperation" zu "erniedrigen". Aus Potenzieren und Radizieren wird Multiplikation und Division. Aus Multiplikation bzw. Division werden Addition bzw. Subtraktion.

Dies war vor der Erfindung vom Taschenrechner vor allem in der Astronomie und der Seefahrt von so großer Bedeutung, dass Mathematiker ihr ganzes Berufsleben damit verbrachten Logarithmustabellen zu erstellen, um es den Astronomen zu ermöglichen, einfache Multiplikationen oder Divisionen statt aufwendig Potenzen bzw. Wurzeln zu berechnen.

• Multiplikation → Addition: \({\log _a}\left( {u \cdot v} \right) = {\log _a}\left( u \right) + {\log _a}\left( v \right)\)
• Division → Subtraktion: \({\log _a}\dfrac{u}{v} = {\log _a}\left( u \right) - {\log _a}\left( v \right)\)
• Potenzieren → Multiplikation: \({\log _a}\left( {{u^r}} \right) = r \cdot {\log _a}\left( u \right)\)
• Wurzelziehen → Division: \({\log _a}\left( {\root r \of u } \right) = \dfrac{1}{r} \cdot {\log _a}\left( u \right)\)

Grundlegende Rechenregeln für Logarithmen

\({}^a\log \left( {u \cdot v} \right) = {}^a\log u + {}^a\log v\)

Logarithmus eines Quotienten

Der Logarithmus eines Quotienten, ist gleich der Differenz der Logarithmen seines Dividenden und seines Divisors. Rechnet man mit Logarithmen führt man eine Division auf eine wesentlich einfachere Subtraktion zurück.

\({}^a\log \dfrac{u}{v} = - {}^a\log \dfrac{v}{u} = {}^a\log u - {}^a\log v\)

Logarithmus einer Potenz

Der Logarithmus einer Potenz, ist gleich dem Produkt aus dem Exponenten und dem Logarithmus seiner Basis. Rechnet man mit Logarithmen führt man das Potenzieren von u^r auf eine wesentlich einfachere Multiplikation zurück.

\({}^a\log {u^r} = r \cdot {}^a\log u\)

Logarithmus einer Wurzel

Der Logarithmus einer Wurzel, ist gleich dem Quotienten aus dem Logarithmen seines Radikanden und aus dem Wert des Wurzelexponenten. Rechnet man mit Logarithmen führt man das Wurzelziehen auf eine wesentlich einfachere Division zurück

\({}^a\log \root n \of u = \dfrac{{{}^a\log u}}{n}\)

Logarithmus dessen Basis ein Quotient ist

Der Logarithmus dessen Basis ein Quotient ist, ist gleich dem mit -1 multiplizierten Logarithmus, dessen Basis der Kehrwert des Quotienten ist.

\({}^{\dfrac{1}{a}}\log u = - {}^a\log u\)