Vektoranalysis

Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit

Bild

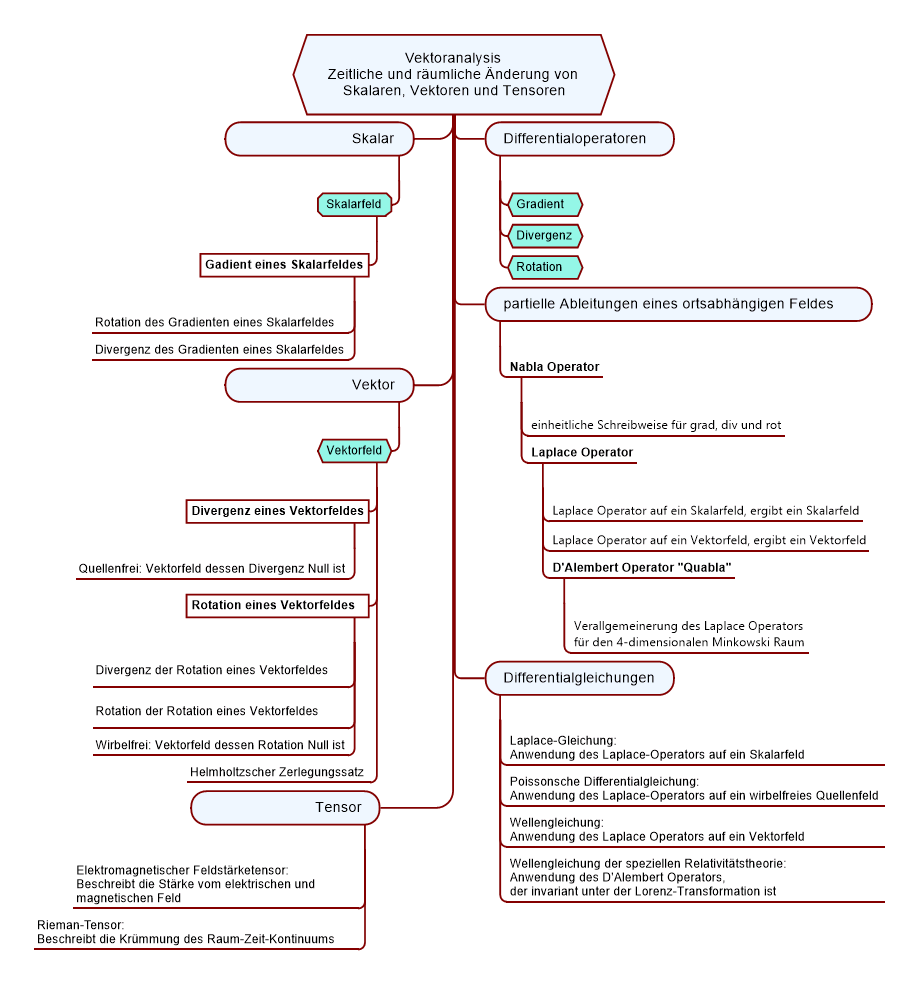
Vektoranalysis

Die Vektoranalysis ist ein Teilgebiet der Mathematik, welches sich mit Skalaren, Vektoren und Tensoren, sowie deren Änderung in Raum und Zeit beschäftigt.

In der Physik spricht man in diesem Zusammenhang von Feldern, z.B.: \(\vec D{\mkern 1mu} - {\mkern 1mu} \vec E{\mkern 1mu} - {\mkern 1mu} \vec B{\mkern 1mu} - {\mkern 1mu} \vec H\) in der Elektrodynamik, in der Mathematik von Funktionen, z.B.: \(\overrightarrow f = \overrightarrow f \left( {x,y,z} \right)\). Die Vektoranalysis verbindet die Vektorrechnung mit der Analysis und dort speziell mit der Infinitesimalrechnung (Differential- und Integralrechnung).

Ein Feld ist eine Energieform, die den Raum erfüllt. Felder können sich mit endlicher Geschwindigkeit ausbreiten, wobei ihre Dynamik durch Feldgleichungen beschrieben wird.

Zeitlich unveränderliche räumliche Felder benötigen zu ihrer Beschreibung eine Funktion mit den 3 Variablen \(\overrightarrow f = \overrightarrow f \left( {x,y,z} \right)\) , um das Feld in jedem Punkt im 3-dimensionalen Raum beschreiben zu können. Will man eine derartige Funktion ableiten, so bedient man sich der partiellen Ableitung. Bei der partiellen Ableitung leitet man jeweils nach einer der unabhängigen Variablen ab, und behandelt die anderen unabhängigen Variablen wie Konstante.

Ein wichtiges Anwendungsgebiet der Vektoranalysis sind elektromagnetische Felder. Die maxwellschen Gleichungen, in Integral- und Differentialform zur Beschreibung des elektromagnetischen Feldes, sind fundamentale Anwendungsgebiete der Vektoranalysis in der physikalischen Praxis.

Ein weiteres wichtiges Anwendungsgebiet der Vektoranalysis sind die 4 fundamentalen Wechselwirkungen, die beschreiben, wie physikalische Objekte einander beeinflussen, samt dem Higgs-Feld, welches dafür sorgt, dass Teilchen ihre Masse erhalten.

Die Verwendung von Tensoren, speziell von Minkowski-Raumzeit-Tensoren ermöglichte eine kompakte Darstellung der Lorenz-Transformation in der speziellen Relativitätstheorie und die Formulierung der Beziehung zwischen der Gravitationskraft einerseits und der Krümmung der Raumzeit andererseits, zufolge der Einstein-Tensorgleichung der allgemeinen Relativitätstheorie.

Felder, durch Tensoren dargestellt

Ein Tensor ist ein mathematischer Begriff zur Verallgemeinerung von Skalaren, Vektoren und Matrizen. Der Rang eines Tensors ergibt sich aus der Anzahl der Indizes, die benötigt werden, um ein Element zu referenzieren.  

Man kann Felder nach ihrem Rang wie folgt unterscheiden:

• Skalarfelder
  Ein Skalarfeld ist ein Tensor des Rangs 0, da es nur einen Wert gibt, und somit kein Index nötig ist.
  • Temperatur im Raum
  • Higgs Feld
• Vektorfelder
  Ein Vektorfeld ist ein Tensor des Rangs 1, da nur 1 Index zur Beschreibung nötig ist.
  • Die elektromagnetischen Felder \(\vec D{\mkern 1mu} - {\mkern 1mu} \vec E{\mkern 1mu} - {\mkern 1mu} \vec B{\mkern 1mu} - {\mkern 1mu} \vec H\) , z.B.: \(\overrightarrow {{E_x}} ,\overrightarrow {{E_y}} ,\overrightarrow {{E_z}} \)
  • Feld der schwachen Wechselwirkung
  • Feld der starken Wechselwirkung
• Tensorfelder
  Matrizen sind Tensor vom Rang >1, da 2 oder mehr Indizes zur Beschreibung der Elemente nötig sind.
  • Elektromagnetischer Feldstärkentensor \({F^{\mu \upsilon }}\) ist ein Tensor des Rangs 2, der sowohl die Stärke des elektrischen Feldes E als auch die Stärke des magnetischen Feldes B umfasst.
  • Riemann-Tensor zur Beschreibung der Krümmung des Raum-Zeit-Kontinuums ist ein Tensor des Rangs 4.

Wir verwenden folgende Schreibweise:

• s steht für ein Skalarfeld, in der Literatur wird auch gerne f verwendet
• \(\overrightarrow v \) steht für ein Vektorfeld, in der Literatur wird auch gerne F verwendet
• T_ij unter Verwendung von fetten Buchstaben und Indizes steht für ein Tensorfeld

Differentialoperatoren

Ein Differentialoperator ist eine Abbildungsvorschrift, bei der einer Ausgangsfunktion eine andere Funktion zugeordnet wird, die partielle Ableitungen der Ausgangsfunktion hat.

So bildet etwa der Differentialoperator \(\dfrac{d}{{dx}}\) eine differenzierbare Funktion \(f\left( x \right)\) auf deren 1. Ableitung ab:

\(f\left( x \right) \to \dfrac{d}{{dx}} \to f'\)

Wir werden nun folgende Differentialoperatoren besprechen:

• Gradient, gibt die Richtung des steilsten Anstiegs des Skalarfeldes in Form eines Vektors an
• Divergenz, ist ein Maß für die Existenz von Quellen oder Senken in einem Vektorfeld
• Rotation, ist ein Maß für Drehbewegungen bzw. für die Wirbel des Vektorfeldes.

Zur Vereinfachung der Schreibweise von partiellen Ableitungen dienen folgende Differentialoperatoren:

• Nabla-Operator, entspricht dann der ersten partiellen Ableitung eines ortsabhängigen Feldes und vereinheitlicht die Schreibweise für Gradient, Divergenz und Rotation
• Laplace-Operator, entspricht dann der zweiten partiellen Ableitung eines ortsabhängigen Feldes.
• D’Alembert-Operator, stellt eine Verallgemeinerung des Laplace Operators für den 4-dimensionalen Minkowski Raum dar und ist invariant unter der Laplace-Transformation

Gradient

Der Gradient ist jener Differentialoperator, der einem räumlichen Skalarfeld \(s \to s\left( {x,y,z} \right)\) den Vektor der partiellen Ableitungen des Skalarfeldes zuordnet. Dieser Vektor heißt Gradient und kann mit dem Nabla-Operator einfach angeschrieben werden.

\(grad\,s = \overrightarrow \nabla s = \left( {\begin{array}{*{20}{c}} {{\partial _x}s}\\ {{\partial _y}s}\\ {{\partial _z}s} \end{array}} \right)\)

Umgekehrt formuliert, bildet der Differentialoperator, diesmal als Zeilenvektor geschrieben, \(\left( {\dfrac{\partial }{{\partial x}},\dfrac{\partial }{{\partial y}},\dfrac{\partial }{{\partial z}}} \right)\) ein zeitlich unveränderliches räumliches Skalarfeld \(s = s\left( {x,y,z} \right)\)auf dessen Gradienten – ein Vektorfeld - ab:

\(s\left( {x,y,z} \right) \to \left( {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}}\\ {\dfrac{\partial }{{\partial y}}}\\ {\dfrac{\partial }{{\partial z}}} \end{array}} \right) \to grad\,s = \overrightarrow \nabla \,s\)

Rechenregeln:

\(\begin{array}{l} \overrightarrow \nabla \left( {f + g} \right) = \overrightarrow \nabla f + \overrightarrow \nabla g\\ \overrightarrow \nabla \left( {f \cdot g} \right) = f \cdot \overrightarrow \nabla g + g \cdot \overrightarrow \nabla f \end{array}\)

Beispiel:  Anwendung des Nabla-Operators auf eine Funktion mit 3 unabhängigen Variablen, bzw. Bildung des Gradienten der Funktion

\(\begin{array}{l} s\left( {x,y,z} \right) = {x^2} + {y^2} + {z^2}\\ grad\,s = ?\\ \\ \dfrac{{\partial s}}{{\partial x}} = 2x + 0 + 0\\ \dfrac{{\partial s}}{{\partial y}} = 0 + 2y + 0\\ \dfrac{{\partial s}}{{\partial z}} = 0 + 0 + 2z\\ \\ \overrightarrow \nabla s = grad\,s = \left( {\begin{array}{*{20}{c}} {2x}\\ {2y}\\ {2z} \end{array}} \right) = 2x \cdot \overrightarrow i + 2y \cdot \overrightarrow j + 2z \cdot \overrightarrow k \end{array}\)

mit

\(\overrightarrow i ,\overrightarrow j {\text{ und }}\overrightarrow k {\text{ : Basisvektoren}}\)

Divergenz

Der Divergenz ist jener Differentialoperator, der einem räumlichen Vektorfeld \(\overrightarrow v \to \overrightarrow v \left( {x,y,z} \right)\) die Summe der partiellen Ableitung der x,y,z-Koordinate zuordnet. Diese Summe ist ein Skalar. Sie ist ein Maß für die Quellenstärke des Vektorfeldes in einem bestimmten Punkt. 

Mathematisch ist die Divergenz das Skalarprodukt aus dem Nabla-Vektor und dem räumlichen Vektorfeld.

\(div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v = \sum\limits_{i = x}^z {{\partial _i}{v_i}} = \dfrac{{\partial {v_x}}}{{\partial x}} + \dfrac{{\partial {v_y}}}{{\partial y}} + \dfrac{{\partial {v_z}}}{{\partial z}}\)

Rechenregeln:

\(\begin{array}{l} div\left( {\overrightarrow u + \overrightarrow v } \right) = div\overrightarrow u + div\overrightarrow v \\ div\left( {s \cdot \overrightarrow v } \right) = s \cdot div\overrightarrow v + \left( {\overrightarrow {\nabla s} } \right) \cdot \overrightarrow v \\ div\left( {\overrightarrow u \times \overrightarrow v } \right) = \overrightarrow v \cdot rot\overrightarrow u - \overrightarrow u \cdot rot\overrightarrow v \end{array}\)

Beispiel:  Anwendung des Skalarprodukts aus dem Nabla-Operator und einer Vektorfunktion mit 3 unabhängigen Variablen, bzw. Bildung der Divergenz der Funktion.

\(\begin{array}{l} \overrightarrow v \left( {x,y,z} \right) = \left( {\begin{array}{*{20}{c}} {3xz - 4{e^{2z}}}\\ {2z + 2x{e^{ - 4y}}}\\ {3x{y^2}z} \end{array}} \right)\\ div\,\overrightarrow v = ?\\ \\ div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v \\ NR.:\\ \dfrac{{\partial {v_x}}}{{\partial x}} = \dfrac{d}{{dx}} \cdot \left( {3xz - 4{e^{2z}}} \right) = 3z\\ \dfrac{{\partial {v_y}}}{{\partial y}} = \dfrac{d}{{dy}} \cdot \left( {2z + 2x{e^{ - 4y}}} \right) = - 4 \cdot 4x \cdot {e^{ - 4y}}\\ \dfrac{{\partial {v_z}}}{{\partial z}} = \dfrac{d}{{dz}} \cdot \left( {3x{y^2}z} \right) = 3x{y^2}\\ \\ div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v = \sum\limits_{i = x}^z {{\partial _i}{v_i}} = 3z - 16x \cdot {e^{ - 4y}} + 3x{y^2} \end{array}\)

Setzt man nun für einen Punkt des Vektorfeldes ein, gibt es 3 Möglichkeiten:

\(\eqalign{ & P\left( {{x_P}|{y_P}|{z_p}} \right) \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 > 0 \to {\text{P ist Quelle}} \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 < 0 \to {\text{P ist Senke}} \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 = 0 \to {\text{P ist weder Quelle noch Senke}} \cr} \)

Rotation

Die Rotation ist jener Differentialoperator, der einem räumlichen Vektorfeld \(\overrightarrow v \to \overrightarrow v \left( {x,y,z} \right)\) ein anderes räumliches Vektorfeld gemäß dem Kreuzprodukt aus dem Gradienten des Vektorfeldes und dem Vektorfeld selbst zuordnet.

Mathematisch ist die Rotation das Kreuzprodukt aus dem Nabla-Vektor und dem räumlichen Vektorfeld.

\(rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v = \left( {\dfrac{{\partial {v_z}}}{{\partial y}} - \dfrac{{\partial {v_y}}}{{\partial z}},\dfrac{{\partial {v_x}}}{{\partial z}} - \dfrac{{\partial {v_z}}}{{\partial x}},\dfrac{{\partial {v_y}}}{{\partial x}} - \dfrac{{\partial {v_x}}}{{\partial y}}} \right)\)

Rechenregeln:

\(\begin{array}{l} rot\left( {\overrightarrow u + \overrightarrow v } \right) = rot\overrightarrow u + rot\overrightarrow v \\ rot\left( {s \cdot \overrightarrow v } \right) = s \cdot rot\overrightarrow v + \left( {\overrightarrow \nabla s} \right) \times \overrightarrow v \\ rot\left( {\overrightarrow u \times \overrightarrow v } \right) = \left( {\overrightarrow v \circ \overrightarrow \nabla } \right)\overrightarrow u - \overrightarrow v \left( {\overrightarrow \nabla \circ \overrightarrow u } \right) - \left( {\overrightarrow u \circ \overrightarrow \nabla } \right)\overrightarrow v + \overrightarrow u \left( {\overrightarrow \nabla \circ \overrightarrow v } \right) \end{array}\)

Beispiel:  Anwendung des Kreuzprodukts aus dem Nabla-Operator und einer Vektorfunktion mit 3 unabhängigen Variablen, bzw. Bildung der Divergenz der Funktion.

\(\begin{array}{l} \overrightarrow v \left( {x,y,z} \right) = \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x^2} + {z^3}}\\ {{x^2} + {y^3}}\\ {{y^2} + {z^3}} \end{array}} \right)\\ rot\,\overrightarrow v = ?\\ \\ rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v \\ rot\,\overrightarrow v = \left( {\begin{array}{*{20}{c}} {{\partial _y}{v_z} - {\partial _z}{v_y}}\\ {{\partial _z}{v_x} - {\partial _x}{v_z}}\\ {{\partial _x}{v_y} - {\partial _y}{v_x}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\dfrac{{d\left( {{y^2} + {z^3}} \right)}}{{dy}} - \dfrac{{d\left( {{x^2} + {y^3}} \right)}}{{dz}}}\\ {\dfrac{{d\left( {{x^2} + {z^3}} \right)}}{{dz}} - \dfrac{{d\left( {{y^2} + {z^3}} \right)}}{{dx}}}\\ {\dfrac{{d\left( {{x^2} + {y^3}} \right)}}{{dx}} - \dfrac{{d\left( {{x^2} + {z^3}} \right)}}{{dy}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {2y - 0}\\ {3{z^2} - 0}\\ {2x - 0} \end{array}} \right)\\ \\ rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v = \left( {\begin{array}{*{20}{c}} {2y}\\ {3{z^2}}\\ {2x} \end{array}} \right) \end{array}\)

Das bedeutet, dass sich jeder Punkt des räumlichen Vektorfeldes um die Rotationsachse \(\left( {\begin{array}{*{20}{c}} {2y}\\ {3{z^2}}\\ {2x} \end{array}} \right)\) dreht.

Mit Hilfe der Differentialoperatoren Gradient (grad), Divergenz (div) und Rotation (rot) kann man die Eigenschaften von Feldern untersuchen.

• Wendet man Gradient auf ein skalares Feld an, erhält man ein Vektorfeld.
• Wendet man Divergenz auf ein Vektorfeld an, erhält man ein Skalarfeld.
• Wendet man Rotation auf ein Vektorfeld an, erhält man wieder ein Vektorfeld.

grad, div und rot sind unterschiedliche Arten der Differentiation im Zusammenhang mit der Vektorrechnung.

Zur Vereinfachung der Schreibweise partieller Ableitungen bedient sich die Vektoranalysis weiterer Operatoren

Differentialoperator Nabla

Der Nabla-Operator ist ein vektorieller Differentialoperator und hat alleinstehend keine Bedeutung. Er muss auf ein Skalar s oder einen Vektor \(\overrightarrow v \) angewendet werden und entspricht dann der ersten partiellen Ableitung eines ortsabhängigen Feldes.

Der Nabla-Operator fasst in einem Symbol \(\overrightarrow \nabla \) die drei partiellen Differentiationen nach der jeweiligen Ortskoordinate x, y bzw. z zusammen.

\(\vec \nabla = \left( {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}}\\ {\dfrac{\partial }{{\partial y}}}\\ {\dfrac{\partial }{{\partial z}}} \end{array}} \right)\)

Mit Hilfe vom Differentialoperator Nabla ist es möglich die Operatoren grad, div und rot in einer einheitlichen Form anzuschreiben.

\(\begin{array}{*{20}{l}} {grad\,s = \overrightarrow \nabla s}\\ {div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v }\\ {rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v } \end{array}\)

Laplace Operator

Der Laplace Operator ist ein Differentialoperator und hat alleinstehend keine Bedeutung. Er entspricht der zweifachen Anwendung des Nabla Operators. Er muss auf ein Skalar s oder einen Vektor \(\overrightarrow v \) angewendet werden und entspricht dann der zweiten partiellen Ableitung eines jeweiligen ortsabhängigen Feldes.

\(\overrightarrow \nabla \circ \overrightarrow \nabla = {\overrightarrow \nabla ^2} = \Delta {\rm{ }}...{\rm{Laplace Operator}}\)

\({\rm{\Delta }} = \left( {\dfrac{{{\partial ^2}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}}}{{\partial {z^2}}}} \right)\)

Laplace Operator auf ein Skalarfeld angewendet

Wendet man den Laplace Operator auf ein Skalarfeld s an, ist das Resultat wieder ein Skalar.

\({\nabla ^2}s = {\rm{\Delta s}} = \dfrac{{{\partial ^2}s}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}s}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}s}}{{\partial {z^2}}}\)

• Ein Beispiel für die Anwendung des Laplace Operators auf ein Skalarfeld ist die Laplace-Gleichung. Skalarfelder \(s\left( {x,y,z} \right)\) die der Laplacegleichung \({\rm{\Delta s}} = 0 \) genügen, sind quellen- und wirbelfrei, etwa die Temperaturverteilung in einem homogenen Medium.
  \(\begin{array}{*{20}{l}} {\overrightarrow \nabla s = grad{\mkern 1mu} s}\\ {div\,\overrightarrow s = div\left( {grad{\mkern 1mu} {\mkern 1mu} s} \right) = {\rm{\Delta s}} = 0 \to {\rm{Quellenfreiheit}}}\\ {rot\,\overrightarrow s = rot\left( {grad{\mkern 1mu} {\mkern 1mu} s} \right) = 0 \to {\rm{Wirbelfreiheit}}} \end{array}\)

• Ein Beispiel für die Anwendung des Laplace-Operators auf ein wirbelfreies Quellenfeld, etwa das elektrische Potential, ist die poissonsche Differentialgleichung
  \({\nabla ^2}\varphi = {\rm{\Delta }}\varphi = \dfrac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\varphi }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\varphi }}{{\partial {z^2}}} = - q\)
  der zufolge der Laplace-Operator des elektrischen Potentials Phi gleich der negativen Ladungsdichte q ist. Diese Gleichung beschreibt, wie jede punktförmige Ladung Q an einem Punkt im Raum, einen Beitrag zum Potential Phi an einem anderen Punkt im Raum erbringt.

Laplace Operator auf ein Vektorfeld angewendet

Wendet man den Laplace Operator auf ein Vektorfeld \(\overrightarrow v \) an, ist das Resultat wieder ein Vektor.
\({\nabla ^2}\overrightarrow v = {\rm{\Delta }}\overrightarrow v = \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {z^2}}}\)

Ein Beispiel für die Anwendung des Laplace Operators auf ein Vektorfeld ist die Wellengleichung.

Die Wellengleichung beschreibt die Ausbreitung von Wellen in Raum und Zeit mittels einer partiellen Differenzialgleichung. Sie besagt, dass die 2. räumliche Ableitung der Auslenkung proportional zur 2. zeitlichen Ableitung der Auslenkung ist, wobei der Proportionalitätsfaktor 1/c² beträgt. Der Laplace Operator ist eine Kurzschreibweise für die 2. räumliche Ableitung.
\(\begin{array}{l} \psi = \psi \left( {x,y,z,t} \right)\\ \dfrac{{{\partial ^2}\psi }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\psi }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\psi }}{{\partial {z^2}}} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}}\\ \Delta \psi = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}}\\ \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}} - \Delta \psi = 0 \end{array}\)

D’Alembert-Operator Quabla

Der D’Alembert Operator namens "Quabla", auch als Wellenoperator bezeichnet, ist ein hyperbolischer Differentialoperator. Er ist eine lineare Kombination aus der zeitlichen Ableitung und dem Laplace-Operator.

Er stellt eine Verallgemeinerung des Laplace Operators für den 4-dimensionalen Minkowski Raum dar und findet daher im Rahmen der speziellen Relativitätstheorie (SRT) Anwendung. Der D’Alembert Operator ist invariant unter der Lorenz-Transformation.

\(\square = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - {\Delta} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - \dfrac{\partial }{{\partial {x^2}}} - \dfrac{\partial }{{\partial {y^2}}} - \dfrac{\partial }{{\partial {z^2}}}\)

Manche Autoren schreiben obige Gleichung gleichwertig auch wie folgt an

\(\square = {\nabla ^2} - \dfrac{1}{{{c^2}}}\dfrac{{{\partial ^2}}}{{\partial {t^2}}}\)

wobei:

c … Lichtgeschwindigkeit

• Die Wellengleichung in der speziellen Relativitätstheorie mit dem D’Alembert-Operator formuliert lautet: 
  \(\eqalign{ & \psi = \psi \left( {x,y,z,t} \right) \cr & \square \psi = 0 \cr} \)
  Diese Gleichung beschreibt, wie sich Wellen (etwa elektromagnetische Wellen) in der Raumzeit ausbreiten. Sie besagt, dass die Wellenfunktion in allen 4 Raumzeit-Koordinaten (x,y,z und t) glatt ist und keine Divergenz oder Rotation hat.

Skalarfeld

In einem Skalarfeld wird jedem Punkt des vom Feld erfüllten Raums ein bestimmter Absolutwert \({s_P} = s\left( {{P_x},{P_y},{P_z}} \right)\) zugeordnet. 

\(s = s\left( {x,y,z} \right)\)

Beispiele für Skalarfelder sind die Temperatur in einem Raum oder das Potential.

Illustration eines Skalarfeldes

Bild

Gradient eines Skalarfeldes

Das Produkt des Nabla-Operators mit einem Skalarfeld f(x,y,z) nennt man Gradient. Der Gradient ist ein Vektor, dessen x,y,z-Komponenten sich aus den 3 ersten partiellen Ableitung (nach x, nach y, nach z) der Gleichung vom Skalarfeld ergeben.

Der Gradient gibt die Richtung des steilsten Anstiegs des Skalarfeldes in Form eines Vektors an. Der Betrag des Gradienten gibt, wie bei Betrag eines x-beliebigen Vektors, die Größe der Änderung an.

Das Resultat ist ein Vektorfeld. Der Gradient ordnet einem Skalarfeld, welches naturgemäß keine Richtung aber eine Ortsabhängigkeit hat, ein Vektorfeld zu, welches die Richtung der größten Zunahme des Skalarfelds anzeigt.

\(\eqalign{ & \vec \nabla s = \operatorname{grad} s = \left( {\dfrac{{\partial s}}{{\partial x}},\dfrac{{\partial s}}{{\partial y}},\dfrac{{\partial s}}{{\partial z}}} \right) \cr & \left| {\operatorname{grad} s} \right| = \sqrt {{{\left( {\dfrac{{\partial s}}{{\partial x}}} \right)}^2} + {{\left( {\dfrac{{\partial s}}{{\partial y}}} \right)}^2} + {{\left( {\dfrac{{\partial s}}{{\partial z}}} \right)}^2}} \cr} \)

Rechenregeln für Gradienten

\(\eqalign{ & \overrightarrow \nabla \left( {{s_1} + {s_2}} \right) = \overrightarrow \nabla {s_1} + \overrightarrow \nabla {s_2} \cr & \overrightarrow \nabla \left( {{s_1} \cdot {s_2}} \right) = {s_1} \cdot \overrightarrow \nabla {s_2} + {s_2} \cdot \overrightarrow \nabla {s_1} \cr} \)

Der Gradient \(\vec \nabla s = \operatorname{grad} s\) steht senkrecht auf jene Flächen, für die \(s = s\left( {x,y,z} \right) = konst.\) gilt. Wenn die skalare Funktion etwa ein Potential darstellt, bezeichnet man diese Flächen als Äquipotentialflächen und die Richtung der Größten Änderung des Potentials ist senkrecht auf die Äquipotentialfläche.

Illustration vom Gradienten eines Skalarfeldes

Bild

2. Ableitungen von Skalarfeldern

Wendet man Gradient auf ein skalares Feld an, erhält man ein Vektorfeld. Auf dieses Vektorfeld kann man nun die Rotation und die Divergenz anwenden.

Rotation des Gradienten eines Skalarfeldes

Die Rotation des Gradienten eines Skalarfeldes ist Null. Kurz: Skalarfelder sind wirbelfrei.

\({\text{rot}}{\mkern 1mu} {\mkern 1mu} \times {\mkern 1mu} {\mkern 1mu} {\text{grad}}{\mkern 1mu} {\mkern 1mu} s = \overrightarrow \nabla \times \left( {\overrightarrow \nabla s} \right) = 0\)

Divergenz des Gradienten eines Skalarfeldes

Die Divergenz des Gradienten eines Skalarfeldes entspricht der Anwendung vom Laplace-Operator.

\(div\left( {grad{\text{ s}}} \right) = \overrightarrow \nabla \cdot \overrightarrow \nabla s = \Delta s\)

Spezialfall: Ist die Divergenz des Gradienten eines Skalarfeldes null, dann bezeichnet man das Skalarfeld als harmonisch. Bei einem harmonischem Skalarfeld verschwindet in jedem Punkt des Raums die Krümmung des Feldes.

\(div\left( {grad{\text{ s}}} \right) = \overrightarrow \nabla \cdot \overrightarrow \nabla s = \Delta s = 0\)

Beispiel: Harmonisches Skalarfeld

\(\eqalign{ & s\left( {x,y,z} \right) = 2{x^2} - {y^2} - {z^2} \cr & grad{\text{ s = }}\overrightarrow \nabla s = \left( {4x, - 2y, - 2z} \right) \cr & \Delta s = 4 - 2 - 2 = 0 \cr} \)

Vektorfeld

In einem Vektorfeld wird jedem Punkt \(P\left( {{P_x},{P_y},{P_z}} \right)\) des vom Feld erfüllten Raums, ein bestimmter Vektor\(\overrightarrow {{v_P}} = \vec v\left( {{P_x},{P_y},{P_z}} \right)\) zugeordnet.

\(\overrightarrow v = \overrightarrow v \left( {x,y,z} \right)\)

Beispiele für Vektorfelder sind der Wärmefluss oder die elektrische oder magnetische Feldstärke.

Man kann sich ein Vektorfeld räumlich so vorstellen, als würde in jedem Punkt vom Zimmer in dem man sitzt, ein Vektor seinen Anfangspunkt haben. Jeder dieser unendlich vielen Vektoren würde in jene Richtung zeigen, in der sich die Temperatur im Raum am stärksten ändert. Die Länge von jedem der unendlich vielen Vektoren wäre ein Maß dafür, wie stark sich die Temperatur im jeweiligen Raumpunkt ändert. Was wir in den letzten drei Sätzen beschrieben haben, ist das "vektorielle Gradientenfeld vom skalaren Temperaturfeld".

Zu einem Vektorfeld kann man dessen Divergenz (Quellen) und dessen Rotation (Wirbeln) bestimmen. Ein Vektorfeld ist bis auf eine Integrationskonstante eindeutig bestimmt, wenn man dessen Quellen und Wirbel kennt. Die Quellendichte (Divergenz) ist eine skalare Größe, die Wirbeldichte (Rotation) ist eine vektorielle Größe.

Illustration eines Vektorfeldes

Bild

Divergenz eines Vektorfeldes

Das Skalarprodukt vom Nabla-Operator mit einem Vektorfeld \(\overrightarrow v \) nennt man Divergenz. Das Skalarprodukt aus dem Nabla-Vektor und dem Feldvektor ist ein Skalar.

Die Divergenz eines Vektorfeldes ist ein Maß für die Existenz von Quellen oder Senken. Das Resultat ist ein Skalarfeld. Wenn die Divergenz eines Vektorfeldes Null ist, so ist das Vektorfeld quellenfrei.

Elektrische Felder sind ein Beispiel für Quellenfelder, deren Quellen die positiven elektrischen Ladungen und deren Senken die negativen elektrischen Ladungen sind.

\(div\,\vec v = \left( {\dfrac{{\partial {v_x}}}{{\partial x}} + \dfrac{{\partial {v_y}}}{{\partial y}} + \dfrac{{\partial {v_z}}}{{\partial z}}} \right) = \vec \nabla \circ \vec v\)

Die Divergenz eines Vektorfeldes ist ein Skalarfeld, welches für jeden Punkt des Raums angibt, ob dort Feldlinien entstehen, Quelle mit \(div\,\vec v\left( x \right) > 0\) oder verschwinden, Senke mit \(div\,\vec v\left( x \right) < 0\). Die Divergenz ist am Ort einer positiven Punktladung größer null, da dort Feldlinien entstehen.

Rotation eines Vektorfeldes

Das Kreuzprodukt vom Nabla-Operator mit einem Vektorfeld \(\overrightarrow v \) nennt man Rotation. Das Kreuzprodukt aus dem Nabla-Vektor und dem Feldvektor ist ein Vektor. Der Vektor \(rot\overrightarrow v \) bezeichnet die Wirbeldichte des Vektorfeldes \(\overrightarrow v \).

Die Rotation eines Vektorfeldes ist ein Maß für Drehbewegungen bzw. für die Wirbel des Vektorfeldes. Das Resultat ist erneut ein Vektorfeld. Wenn die Rotation eines Vektorfeldes Null ist, so ist das Vektorfeld wirbelfei.

\(rot\,\vec v = \left( {\begin{array}{*{20}{c}} {\dfrac{{\partial {v_z}}}{{\partial y}} - \dfrac{{\partial {v_y}}}{{\partial z}}}\\ {\dfrac{{\partial {v_x}}}{{\partial z}} - \dfrac{{\partial {v_z}}}{{\partial x}}}\\ {\dfrac{{\partial {v_y}}}{{\partial x}} - \dfrac{{\partial {v_x}}}{{\partial y}}} \end{array}} \right) = \vec \nabla \times \vec v\)

Die Rotation eines Vektorfeldes ist ein Vektorfeld, welches angibt, wie stark sich das Vektorfeld \(\overrightarrow v \) n eine bestimmte Koordinatenrichtung ändert. Vektorfelder mit nicht verschwindender Rotation werden Wirbelfelder genannt. Ein Beispiel dafür ist das Magnetfeld.

2. Ableitungen von Vektorfeldern

Divergenz der Rotation eines Vektorfeldes ist immer Null

Der Rotationssatz besagt, dass die Divergenz der Rotation eines Vektorfeldes \(\overrightarrow v \) 

immer Null ist. Das bedeutet, dass die Rotation eines Vektorfeldes nie zu einer Quelle oder Senke führt, oder kurz:

Ein Wirbelfeld ist quellenfrei!
\(div{\mkern 1mu} {\mkern 1mu} rot\,\vec v = \overrightarrow \nabla \circ \left( {\overrightarrow \nabla \times \vec v} \right) = 0\)

Rotation der Rotation eines Vektorfeldes

Die Doppelrotation eines Vektorfeldes ist erneut ein Vektorfeld.

\(rot\,\,rot\overrightarrow v = \overrightarrow \nabla \times \left( {\overrightarrow \nabla \times \overrightarrow v } \right) = \overrightarrow \nabla \left( {\overrightarrow \nabla \circ \overrightarrow v } \right) - \overrightarrow \Delta \circ \overrightarrow v = grad\left( {div\overrightarrow v } \right) - \overrightarrow \Delta \circ \overrightarrow v \)

Fundamentalsatz der Vektoranalysis

• Vektorfelder deren Rotation Null ist, nennt man wirbelfrei.
• Vektorfelder deren Divergenz Null ist, nennt man quellenfrei.

Der Helmholtzsche Zerlegungssatz sagt aus, dass man jedes Vektorfeld \(\overrightarrow v \) als Summe eines wirbelfreien Quellenfeldes \(\overrightarrow {{v_Q}} \) und eines quellenfreien Wirbelfeldes \(\overrightarrow {{v_W}} \) beschreiben kann.

\(\overrightarrow v = \overrightarrow {{v_Q}} + \overrightarrow {{v_W}} \)

Ein allgemeines Vektorfeld ist nur dann eindeutig spezifiziert, wenn sowohl die Quellen- als Wirbeldichten und allfällige Randwerte vorliegen.