Vektorrechnung in der Ebene und im Raum

Vektoralgebra

Die Vektoralgebra beschäftigt sich mit den Grundrechenregeln für Vektoren

Addition zweier Vektoren

Bei der Addition von Vektoren werden die einzelnen Komponenten der Vektoren je Achsenrichtung addiert. Zwei Vektoren werden graphisch addiert, \(\overrightarrow s = \overrightarrow a + \overrightarrow b\) indem man die Vektoren aneinander hängt. Der Summenvektor \(\overrightarrow s\) stellt die Diagonale eines durch die beiden Vektoren aufgespannten Parallelogramms dar.

\(\overrightarrow s = \overrightarrow a + \overrightarrow b = \left( {\begin{array}{*{20}{c}} {{a_x}}\\ {{a_y}}\\ {{a_z}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}}\\ {{b_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{a_x} + {b_x}}\\ {{a_y} + {b_y}}\\ {{a_z} + {b_z}} \end{array}} \right)\)

Rechenregeln für die Vektoraddition

\(\begin{array}{l} \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \\ \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c \\ k \cdot \left( {\overrightarrow a + \overrightarrow b } \right) = k \cdot \overrightarrow a + k \cdot \overrightarrow b \\ \left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \end{array}\)

Illustration zur Addition zweier Vektoren

Subtraktion zweier Vektoren

Bei der Subtraktion von Vektoren werden die einzelnen Komponenten der Vektoren je Achsenrichtung subtrahiert. Zwei Vektoren werden graphisch subtrahiert, \(\overrightarrow d = \overrightarrow a - \overrightarrow b\) indem man den inversen Vektor von \(\overrightarrow b\) (gleich lang wie b, aber umgekehrte Richtung), also – b, addiert. Das Resultat einer Vektorsubtraktion wird als Differenzvektor bezeichnet.

\(\overrightarrow d = \overrightarrow a - \overrightarrow b = \left( {\begin{array}{*{20}{c}} {{a_x}}\\ {{a_y}}\\ {{a_z}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}}\\ {{b_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{a_x} - {b_x}}\\ {{a_y} - {b_y}}\\ {{a_z} - {b_z}} \end{array}} \right)\)

Illustration zur Subtraktion zweier Vektoren

Kommutativgesetz der Vektoralgebra

Das Kommutativgesetz der Vektoralgebra besagt, dass bei der Addition von Vektoren die Reihenfolge der Summanden beliebig vertauscht werden darf.

\(\overrightarrow A + \overrightarrow B = \overrightarrow B + \overrightarrow A \)

Distributivgesetze der Vektoralgebra

Das Distributivgesetz der Vektoralgebra besagt, dass man reelle Zahlen aus einer Summe heraushaben kann, wenn bei dieser Summe ein und der selbe Vektor mit unterschiedlichen reellen Zahlen multipliziert wird.

\(\eqalign{ & m\left( {n\overrightarrow A } \right) = \left( {mn} \right)\overrightarrow A = n\left( {m\overrightarrow A } \right) \cr & \left( {m + n} \right)\overrightarrow A = m\overrightarrow A + n\overrightarrow A \cr & m\left( {\overrightarrow A + \overrightarrow B } \right) = m\overrightarrow A + m\overrightarrow B \cr} \)

Assoziativgesetz der Vektoralgebra

Das Assoziativgesetz der Vektoralgebra besagt, dass bei der Addition von Vektoren die Klammern beliebig gesetzt werden dürfen.

\(\overrightarrow A + \left( {\overrightarrow B + \overrightarrow C } \right) = \left( {\overrightarrow A + \overrightarrow B } \right) + \overrightarrow C \)

Multiplikation von Vektoren

Bei der Multiplikation von Vektoren unterscheidet man zwischen

• Multiplikation eines Vektors mit einem Skalar. Das Resultat ist ein in der Länge veränderter Vektor
• Skalarprodukt als Multiplikation zweier Vektoren. Das Resultat ist ein Skalar. Wichtige Anwendung: Orthogonalitätskriterium und Winkel zwischen 2 Vektoren
• Kreuzprodukt als Multiplikation zweier Vektoren. Das Resultat ist ein dritter Vektor, der auf den beiden Ausgangsvektoren normal steht. Wichtige Anwendung: Parallelitätskriterium und Fläche des von 2 Vektoren aufgespannten Parallelogramms
• Spatprodukt als Multiplikation dreier Vektoren. Dabei wird zuerst das Kreuzprodukt zweier Vektoren gebildet. Mit dem daraus resultierenden Vektor und dem dritten gegebenen Vektor wird anschließend das Skalarprodukt gebildet. Das Resultat ist ein Skalar. Wichtige Anwendung: Volumen eines von 3 Vektoren aufgespannten Körpers

Multiplikation eines Vektors mit einem Skalar

Unter Skalarmultiplikation versteht man die Multiplikation eines Vektor \(\overrightarrow a \) mit einer reellen Zahl λ (Skalar). Der resultierende Vektor hat die λ-fache Länge des Ausgangsvektors. Für negative λ sind der Ausgangsvektor und der resultierende Vektor entgegengesetzt orientiert.

\(\lambda \cdot \overrightarrow a = \left( \matrix{ \lambda \cdot {a_x} \hfill \cr \lambda \cdot {a_y} \hfill \cr} \right)\,\,\,\,\,{\rm{wobei}}\,\,\,\,\,\lambda \overrightarrow a \left\| {\overrightarrow a } \right.\)

\(c \cdot \overrightarrow v = c \cdot \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {c \cdot {v_x}}\\ {c \cdot {v_y}}\\ {c \cdot {v_z}} \end{array}} \right)\)

Rechenregeln im Zusammenhang mit der Multiplikation eines Vektors mit einem Skalar

\(\eqalign{ & \lambda \cdot \left( {\overrightarrow a + \overrightarrow b } \right) = \lambda \cdot \overrightarrow a + \lambda \cdot \overrightarrow b \cr & \left( {\lambda + \mu } \right) \cdot \overrightarrow a = \lambda \cdot \overrightarrow a + \mu \cdot \overrightarrow a \cr & 0 \cdot \overrightarrow a = \overrightarrow 0 \cr}\)

Skalarprodukt

Das Skalarprodukt bzw. das innere Produkt zweier Vektoren ordnet zwei Vektoren eine reelle Zahl zu und wird gebildet, in dem komponentenweise multipliziert wird, und anschließend die Summe der Produkte gebildet wird. Es findet Anwendung bei der Winkelberechnung zwischen 2 Vektoren und beim Orthogonalitätskriterium welches besagt, dass wenn zwei Vektoren senkrecht auf einander stehen, ihr Skalarprodukt gleich Null ist

\( \eqalign{ & \overrightarrow a \circ \overrightarrow b = \left( {\matrix{ {{a_x}} \cr {{a_y}} \cr } } \right) \cdot \left( {\matrix{ {{b_x}} \cr {{b_y}} \cr } } \right) = {a_x} \cdot {b_x} + {a_y} \cdot {b_y} = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \varphi \cr & \cos \varphi = {{\overrightarrow a \circ \overrightarrow b } \over {\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}} = {{{a_x} \cdot {b_x} + {a_y} \cdot {b_y}} \over {\sqrt {{a_x}^2 + {a_y}^2} .\sqrt {{b_x}^2 + {b_y}^2} }} \cr}\)

Orthogonalitätskriterium

2 Vektoren stehen im rechter Winkel zueinander, wenn ihr Skalarprodukt Null ist

\(\eqalign{ & \overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \circ \overrightarrow b = 0 \cr & {a_x}{b_x} + {a_y}{b_y} = 0 \cr}\)

Achtung in \({{\Bbb R}^3}\):

• Das Skalarprodukt im 3-dimensionalen Raum macht eine Aussage darüber, ob die beiden Geraden im rechten Winkel auf einander stehen.
• Es macht aber keine Aussage darüber, ob die beiden Geraden in einer Ebene liegen und einander daher schneiden, oder ob sie in 2 parallelen Ebenen liegen und daher windschief zu einander sind.

Winkel zwischen 2 Vektoren

Zwischen zwei Vektoren kann man zwei Winkel einzeichnen, einen innen- und einen außenliegenden Winkel. Wenn nichts Gegenteiliges gesagt wird, ist immer der Innenwinkel gemeint. Zur Berechnung des Winkels bestimmt man zunächst

• das Skalarprodukt \(\overrightarrow a \circ \overrightarrow b = {a_x} \cdot {b_x} + {a_y} \cdot {b_y}\) der beiden Vektoren,
• danach jeweils den Betrag \(\left| {\overrightarrow a } \right| = \sqrt {{a_x}^2 + {a_y}^2} \) bzw. \(\left| {\overrightarrow b } \right| = \sqrt {{b_x}^2 + {b_y}^2} \) der beiden Vektoren
• und setzt dann in die Formel ein.
• Indem wir den ArkusKosinus nehmen, erhalten wir als Resultat den Winkel in Grad.

Den Kosinus vom Winkel zwischen zwei Vektoren erhält man, indem man das Skalarprodukt der beiden Vektoren durch das Produkt der Beträge der beiden Vektoren dividiert. 

\(\varphi = \arccos \dfrac{{\overrightarrow a \circ \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}\) mit \(\left| {\overrightarrow a } \right| \ne 0;\,\,\,\,\,\left| {\overrightarrow b } \right| \ne 0\)

Rechenregeln im Zusammenhang mit dem Skalarprodukt

Kommutativgesetz
\(\overrightarrow a \circ \overrightarrow b = \overrightarrow b \circ \overrightarrow a \)

Distributivgesetz
\(\overrightarrow a \circ \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a \circ \overrightarrow b + \overrightarrow a \circ \overrightarrow c \)

gemischtes Assoziativgesetz, wobei k ein Skalar ist
\(k \cdot \left( {\overrightarrow a \circ \overrightarrow b } \right) = \left( {k \cdot \overrightarrow a } \right) \circ \overrightarrow b = \overrightarrow a \circ \left( {k \cdot \overrightarrow b } \right)\)

Quadrat eines Vektors bzw. Skalarprodukt eines Vektors mit sich selbst

Betrachten wir den Spezialfall dass \(\overrightarrow b = \overrightarrow a \) , dann gilt:

Das Skalarprodukt eines Vektors mit sich selbst bzw. das Quadrat eines Vektors ist gleich dem Quadrat des Betrags vom Vektor. Wir können das wie folgt zeigen:
\(\begin{array}{l} \overrightarrow a \circ \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \varphi \\ \overrightarrow b = \overrightarrow a \to \cos \left( 0 \right) = 1\\ \overrightarrow a \circ \overrightarrow a = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow a } \right| \cdot 1\\ \overrightarrow a \circ \overrightarrow a = {\overrightarrow a ^2} = {\left| {\overrightarrow a } \right|^2} \end{array}\)

Kreuzprodukt

Für das Kreuzprodukt sind auch die Bezeichnungen vektorielles Produkt bzw. äußeres Produkt üblich Das vektorielle Produkt zweier Vektoren ist ein (dritter) Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht. (Rechtssystem).

\(\eqalign{ & \overrightarrow c = \overrightarrow a \times \overrightarrow b = \left( {\matrix{ {{a_x}} \cr {{a_y}} \cr {{a_z}} \cr } } \right)\times\left( {\matrix{ {{b_x}} \cr {{b_y}} \cr {{b_z}} \cr } } \right) = \left( {\matrix{ {{a_y} \cdot {b_z} - {a_z} \cdot {b_y}} \cr {{a_z} \cdot {b_x} - {a_x} \cdot {b_z}} \cr {{a_x} \cdot {b_y} - {a_y} \cdot {b_x}} \cr } } \right) = \left( {\matrix{ {{c_x}} \cr {{c_y}} \cr {{c_z}} \cr } } \right) \cr & \left| {\overrightarrow c } \right| = \left| {\overrightarrow a \times \overrightarrow b } \right| = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|.\sin \varphi ; \cr}\)

\(\eqalign{ & {\text{mit }}\varphi = \sphericalangle \left( {\overrightarrow a ,\overrightarrow b } \right) & }\)

\(\eqalign{ & \overrightarrow a \times \overrightarrow b \bot \overrightarrow a \cr & \overrightarrow a \times \overrightarrow b \bot \overrightarrow b \cr} \)

Die Bildungsvorschrift für den doch etwas komplizierten Klammerausdruck lautet wie folgt:

Schreibe die Komponenten der beiden Vektoren an und füge die beiden oberen Zeilen unten noch einmal an
\(\begin{array}{*{20}{l}} {{a_x}}&{{b_x}}&{}&{}&{}\\ {{a_y}}&{{b_y}}&{}&{}&{}\\ {{a_z}}&{{b_z}}&{}&{}&{}\\ {{a_x}}&{{b_x}}&{}&{}&{}\\ {{a_y}}&{{b_y}}&{}&{}&{} \end{array}\)
 

Fange in der 1. Spalte in der 2. Zeile an und rechne: "(links oben mal rechts unten) minus (links unten mal rechts oben)
\(\begin{array}{*{20}{l}} {{a_x}}&{{b_x}}&{}&{{a_y} \cdot {b_z}}&{ - {a_z} \cdot {b_y}}\\ {{a_y}}&{{b_y}}&{}&{}&{}\\ {{a_z}}&{{b_z}}& \Rightarrow &{}&{}\\ {{a_x}}&{{b_x}}&{}&{}&{}\\ {{a_y}}&{{b_y}}&{}&{}&{} \end{array}\)
 

Wiederhole das Ganze in der 1. Spalten in der 3. Zeile
\(\begin{array}{*{20}{l}} {{a_x}}&{{b_x}}&{}&{{a_y} \cdot {b_z}}&{ - {a_z} \cdot {b_y}}\\ {{a_y}}&{{b_y}}&{}&{{a_z} \cdot {b_x}}&{ - {a_x} \cdot {b_z}}\\ {{a_z}}&{{b_z}}& \Rightarrow &{}&{}\\ {{a_x}}&{{b_x}}&{}&{}&{}\\ {{a_y}}&{{b_y}}&{}&{}&{} \end{array}\)
 

Wiederhole das Ganze in der 1. Spalten in der 4. Zeile

​\(\begin{array}{*{20}{l}} {{a_x}}&{{b_x}}&{}&{{a_y} \cdot {b_z}}&{ - {a_z} \cdot {b_y}}\\ {{a_y}}&{{b_y}}&{}&{{a_z} \cdot {b_x}}&{ - {a_x} \cdot {b_z}}\\ {{a_z}}&{{b_z}}& \Rightarrow &{{a_x} \cdot {b_y}}&{ - {a_y} \cdot {b_x}}\\ {{a_x}}&{{b_x}}&{}&{}&{}\\ {{a_y}}&{{b_y}}&{}&{}&{} \end{array}\)

Betrag vom Kreuzprodukt entspricht der Fläche vom Parallelogramm

Der Betrag des Vektors entspricht der Maßzahl der Fläche, des durch die beiden Vektoren aufgespannten Parallelogramms.

\({\rm{A = l}} \cdot {\rm{b = }}\left| {\left( {\overrightarrow a \times \overrightarrow b } \right)} \right| = {\rm{Skalar}}\)

Illustration vom Kreuzprodukt

Parallelitätskriterium

Zwei Vektoren sind dann zueinander parallel, wenn der Betrag von dem Vektor, der sich aus dem Kreuzprodukt ergibt, Null ist
\(\begin{array}{l} \overrightarrow a \times \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a \parallel \overrightarrow b \\ \left| {\overrightarrow a \times \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a \parallel \overrightarrow b \end{array}\)

Zwei Vektoren sind dann zu einander parallel, wenn ein Vektor ein Vielfaches vom anderen Vektor ist.

\(\overrightarrow a \left\| {\overrightarrow b } \right.\,\, \Leftrightarrow \,\,\overrightarrow b = \lambda .\overrightarrow a \Leftrightarrow \left( {\matrix{ {{b_x}} \cr {{b_y}} \cr } } \right) = \left( {\matrix{ {\lambda .{a_x}} \cr {\lambda .{a_y}} \cr } } \right)\)

Rechenregeln im Zusammenhang mit dem​ Kreuzprodukt

Das Kommutativgesetz gilt nicht für das Kreuzprodukt, sondern es besteht folgender Zusammenhang

\(\overrightarrow a \times \overrightarrow b = - \left( {\overrightarrow b \times \overrightarrow a } \right)\)

Das Distributivgesetz gilt für das Kreuzprodukt

\(\eqalign{ & \overrightarrow a \times \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a \times \overrightarrow b + \overrightarrow a \times \overrightarrow c \cr & \left( {\overrightarrow a \times \overrightarrow b } \right) \times \overrightarrow c = \overrightarrow a \times \overrightarrow c + \overrightarrow b \times \overrightarrow c \cr} \)

Darüber hinaus gelten folgende Zusammenhänge

\(\eqalign{ & \overrightarrow a \times \overrightarrow a = 0 \cr & \left( {\lambda \overrightarrow a } \right) \times \overrightarrow b = \lambda \left( {\overrightarrow a \times \overrightarrow b } \right) \cr} \)

Das Spatprodukt

Beim Spatprodukt, auch gemischtes Produkt genannt, wird zuerst von zwei Vektoren das Kreuzprodukt und vom so resultierenden Vektor zusammen mit einem dritten Vektor das Skalarprodukt berechnet. Es dient dazu das Volumen eines von drei Vektoren aufgespannten Körpers zu berechnen. Solch einen Körper nennt man Parallelepiped oder Spat. Die Bezeichnung Spat ist uns aus der Mineralogie (Feldspat) vertraut. Das Spatprodukt dreier Vektoren liefert als Resultat ein Skalar.

\(V = l \cdot b \cdot h = A \cdot h = \left( {\overrightarrow a \times \overrightarrow b } \right) \circ \overrightarrow c = \overrightarrow d \circ \overrightarrow c = {\rm{Skalar}}\)

Geometrische Operationen mittels  Vektorrechnung

Append Regel

Die Append Regel kommt dann zur Anwendung, wenn von einem Anfangspunkt ausgehend ein Vektor hinzugefügt (to append) werden soll und die Koordinaten vom Endpunkt des Vektors gesucht sind. Man spricht dabei von der Punkt-Vektor Form. Die Komponenten vom Ortsvektor des Endpunktes erhält man, indem man je Achsenrichtung die Komponenten des Anfangspunkts und jene des Vektors addiert.

\(Q = P + \overrightarrow v = P + \overrightarrow {PQ} = \left( {\begin{array}{*{20}{c}} {{P_x}}\\ {{P_y}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{Q_x}}\\ {{Q_y}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{P_x} + {v_x}}\\ {{P_y} + {v_y}} \end{array}} \right)\)

Ein Punkt P plus ein Vektor v ergibt einen neuen Punkt Q

Bild

Normalvektor bzw. Orthogonalvektor & Rechts-Kipp-Regel bzw. Links Kipp Regel

In einem zweidimensionalen kartesischen Koordinatensystem kann es zweckmäßig sein, einen Vektor nach rechts bzw. nach links zu kippen, d.h. um \( \pm 90^\circ \) zu drehen. Der so gekippte Vektor steht dann senkrecht auf dem ursprünglichen Vektor, d.h. er wird zum Normalvektor, auch Orthogonalvektor genannt. Ein Beispiel dafür sind Höhenlinien oder Streckensymmetralen bei Dreiecken.

• Bei der Linkskippregel werden die Komponenten vertauscht und bei der oberen Komponente wird auch das Vorzeichen vertauscht. 
• Bei der Rechtskippregel werden die Komponenten vertauscht und bei der unteren Komponente wird auch das Vorzeichen vertauscht.

\(\begin{array}{l} \overrightarrow a = \left( {\begin{array}{*{20}{c}} {{a_x}}\\ {{a_y}} \end{array}} \right)\\ {\overrightarrow n _{_{{\rm{links}}}}} = \left( {\begin{array}{*{20}{c}} { - {a_y}}\\ {{a_x}} \end{array}} \right){\rm{ bzw}}{\rm{. }}{\overrightarrow n _{_{rechts}}} = \left( {\begin{array}{*{20}{c}} {{a_y}}\\ { - {a_x}} \end{array}} \right) \end{array}\)

Bild

Projektionssatz

Der Projektionssatz ist eine geometrische Interpretation vom Skalarprodukt. Dabei wird ein Vektor \(\overrightarrow b\) in zwei Komponenten zerlegt. Die eine Komponente hat den selben Richtungsvektor wie der Vektor \(\overrightarrow a\), die andere Komponente liegt senkrecht dazu. Das skalare Produkt ist definiert als das Produkt der Länge der Projektion von \(\overrightarrow b\)auf \(\overrightarrow a\), also \(\left| {\overrightarrow b } \right|.\cos \varphi\) und der Länge von \(\overrightarrow a\) also \(\left| {\overrightarrow a } \right|\)

Bild

Normalprojektion eines Vektors auf einen anderen Vektor, Vektorprojektionsformel

In der Mechanik ist es oft zweckmäßig Kräfte in Komponenten zu zerlegen, wobei diese Komponenten nicht zwangsläufig parallel zu den Achsen des Koordinatensystems sein müssen. Dazu bedient man sich der Vektorprojektionsformel, wobei \(\left| {\overrightarrow {{b_a}} } \right|\) die Projektion \(\overrightarrow b \)von auf \(\overrightarrow a \) heißt.

• Die Projektion von \(\overrightarrow b\) auf \(\overrightarrow a\), ist der Betrag \(\left| {\overrightarrow {{b_a}} } \right|\), also eine reelle Zahl, die sich wie folgt ergibt: 
  \(\begin{array}{l} \left| {\overrightarrow {{b_a}} } \right| = \dfrac{{\overrightarrow a \circ \overrightarrow b }}{{\left| {\overrightarrow a } \right|}} = \left| {\dfrac{{{a_x} \cdot {b_x} + {a_y} \cdot {b_y}}}{{\sqrt {{{\left( {{a_x}} \right)}^2} + {{\left( {{a_y}} \right)}^2}} }}} \right|\\ {\rm{wobei }}0^\circ \le \varphi \le 90^\circ \end{array}\)

• Die Längskomponente von Vektor b in Richtung vom Vektor a, das ist der Vektor \(\overrightarrow {{b_a}}\),  ergibt sich zu
  \(\overrightarrow {{b_a}} = \dfrac{{\overrightarrow a \circ \overrightarrow b }}{{{{\left| {\overrightarrow a } \right|}^2}}} \cdot \overrightarrow a \)

Im Zähler vom Bruch steht das Skalarprodukt, also eine reelle Zahl, im Nenner vom Bruch steht das Quadrat vom Betrag, also ebenfalls eine reelle Zahl, womit der Bruch selbst ein Skalierungsfaktor für den Vektor \(\overrightarrow a\) ist. Das macht Sinn, denn es ist ja genau jener Anteil von \(\overrightarrow b\) gesucht, der in Richtung von \(\overrightarrow a\) wirkt.

Bild

Mittelpunkt einer Strecke bzw. Halbierungspunkt zwischen 2 Punkten

Den Mittelpunkt der Strecke von A nach B erhält man, indem man jeweils separat die x, y und z-Komponenten der beiden Punkte A, B addiert und anschließend durch 2 dividiert.

\(\begin{array}{l} A\left( {{A_x}\left| {{A_y}\left| {{A_z}} \right.} \right|} \right),\,\,\,\,\,B\left( {{B_x}\left| {{B_y}\left| {{B_z}} \right.} \right.} \right)\\ {H_{\overrightarrow {AB} }} = {M_{\overrightarrow {AB} }} = A + \dfrac{1}{2}\overrightarrow {AB} = \dfrac{1}{2} \cdot \left( {\begin{array}{*{20}{c}} {{A_x} + {B_x}}\\ {{A_y} + {B_y}}\\ {{A_z} + {B_z}} \end{array}} \right)\\ {H_{AB}}\left( {\dfrac{{{A_x} + {B_x}}}{2}\left| {\dfrac{{{A_y} + {B_y}}}{2}\left| {\dfrac{{{A_z} + {B_z}}}{2}} \right.} \right.} \right) \end{array}\)

Teilungspunkt einer Strecke

Der Teilungspunkt T ist jener Punkt, der die Strecke von A nach B im Verhältnis λ teilt.

\(T = A + \lambda \cdot \overrightarrow {AB} = \left( {1 - \lambda } \right)A + \lambda B\)

Schwerunkt eines Dreiecks

Um die Koordinaten vom Schwerpunkt eines Dreiecks zu berechnen, dessen 3 Eckpunkte gegeben sind, addiert man jeweils für jeden der 3 Eckpunkte gesondert die x, y und z-Komponenten und dividiert anschließend die jeweilige Summe durch 3.

Gegeben sind drei Punkte im Raum
\(A\left( {{A_x}\left| {{A_y}\left| {{A_z}} \right.} \right|} \right),\,\,\,\,\,B\left( {{B_x}\left| {{B_y}\left| {{B_z}} \right.} \right.} \right),\,\,\,\,\,C\left( {{C_x}\left| {{C_y}\left| {{C_z}} \right.} \right.} \right)\)

für deren Schwerpunkt gilt

\(\overrightarrow {OS} = \dfrac{1}{3} \cdot \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)

\(S = \dfrac{1}{3}\left( {A + B + C} \right) = \dfrac{1}{3} \cdot \left( {\begin{array}{*{20}{c}} {{A_x} + {B_x} + {C_x}}\\ {{A_y} + {B_y} + {C_y}}\\ {{A_z} + {B_z} + {C_z}} \end{array}} \right)\)

\({S_{ABC}} = \left( {\dfrac{{{A_x} + {B_x} + {C_x}}}{3}\left| {\dfrac{{{A_y} + {B_y} + {C_y}}}{3}\left| {\dfrac{{{A_z} + {B_z} + {C_z}}}{3}} \right.} \right.} \right) \)

Flächeninhalt des von 2 Vektoren aufgespannten Parallelogramms

Das vektorielle Produkt zweier Vektoren ist ein dritter Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und dessen Betrag der Fläche des durch die beiden Vektoren aufgespannten Parallelogramms entspricht.

\(\begin{array}{l} A = \left| {\overrightarrow a \times \overrightarrow b } \right|\\ A = \left| {\left( {\begin{array}{*{20}{c}} {{a_x}}&{{b_x}}\\ {{a_y}}&{{b_y}} \end{array}} \right)} \right| = \left| {{a_x} \cdot {b_y} - {b_x} \cdot {a_y}} \right| \end{array}\)

Flächeninhalt des von 2 Vektoren aufgespannten Dreiecks

Die Fläche des von 2 Vektoren aufgespannten Dreiecks entspricht dem halben Betrag vom Kreuzprodukt der beiden Vektoren. Das Kreuzprodukt zweier Vektoren ist ein dritter Vektor, der senkrecht auf die von den beiden Vektoren aufgespannte Ebene steht und dessen Betrag der Fläche des durch die beiden Vektoren aufgespannten Parallelogramms entspricht. Die Fläche des aufgespannten Dreiecks ist genau die Hälfte der Fläche vom aufgespannten Parallelogramm.

\(\begin{array}{l} {A_\Delta } = \dfrac{1}{2} \cdot \left| {\overrightarrow a \times \overrightarrow b } \right|\\ {A_\Delta } = \dfrac{1}{2}\left| {\left( {\begin{array}{*{20}{c}} {{a_x}}&{{b_x}}\\ {{a_y}}&{{b_y}} \end{array}} \right)} \right| = \dfrac{1}{2}\left| {{a_x} \cdot {b_y} - {b_x} \cdot {a_y}} \right| \end{array}\)

Linearkombination von Vektoren

Unter der Linearkombination von Vektoren versteht man die Summe von mehreren Vektoren, wobei es sein kann, dass einzelne oder alle Vektoren auch noch mit einem Skalar multipliziert wurden.

\(\overrightarrow s = {\lambda _1} \cdot \overrightarrow {{a_1}} + {\lambda _2} \cdot \overrightarrow {{a_2}} + ... + {\lambda _n} \cdot \overrightarrow {{a_n}} \)

Lineare Abhängigkeit von Vektoren

• Zwei Vektoren sind linear abhängig und daher parallel zu einander, wenn das Kreuzprodukt der beiden Vektoren den Nullvektor ergibt.
   
• Zwei Vektoren sind linear abhängig und daher parallel zu einander, wenn es einen Faktor \(\lambda\)(=Skalar) gibt, mit dem man die Richtungsvektoren \(\left( {\begin{array}{*{20}{c}} {{a_x}}\\ {{a_y}} \end{array}} \right)\) des einen Vektors in die Richtungsvektoren des anderen Vektors durch Multiplikation umrechnen kann \(\left( {\begin{array}{*{20}{c}} {{b_x} = \lambda \cdot {a_x}}\\ {{b_y} = \lambda \cdot {a_y}} \end{array}} \right)\)
   
• Drei Vektoren sind linear abhängig, wenn sie in der selben Ebene liegen, also komplanar sind.
   
• Die drei Vektoren sind dann linear abhängig, wenn sich einer der Vektoren als Linearkombination der beiden anderen Vektoren anschreiben lässt.
  \({\lambda _1} \circ \overrightarrow {{v_1}} + {\lambda _2} \circ \overrightarrow {{v_2}} = \overrightarrow {{v_3}} \)
   
• Mehrere Vektoren sind linear abhängig, wenn sie in einer Ebene liegen und durch Vektoraddition eine geschlossene Vektorkette bilden. Bei einer Vektorkette fallen Anfangs- und Endpunkt zusammen.
   
• Mehrere Vektoren sind dann linear abhängig, wenn sich eine Linearkombination angeben lässt, die den Nullvektor ergibt, wobei mindestens einer der Lambda-Koeffizienten ungleich null sein muss. 
  \({\lambda _1} \circ \overrightarrow {{v_1}} + {\lambda _2} \circ \overrightarrow {{v_2}} + {\lambda _3} \circ \overrightarrow {{v_3}} = \overrightarrow 0 \)

Lineare Unabhängigkeit von Vektoren

• Zwei Vektoren sind dann linear unabhängig, wenn ihr Kreuzprodukt nicht den Nullvektor ergibt
• Mehrere Vektoren sind dann linear unabhängig, wenn sich eine Linearkombination angeben lässt, die den Nullvektor ergibt wobei alle Lambda-Koeffizienten gleich null sein müssen.

Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit

Bild

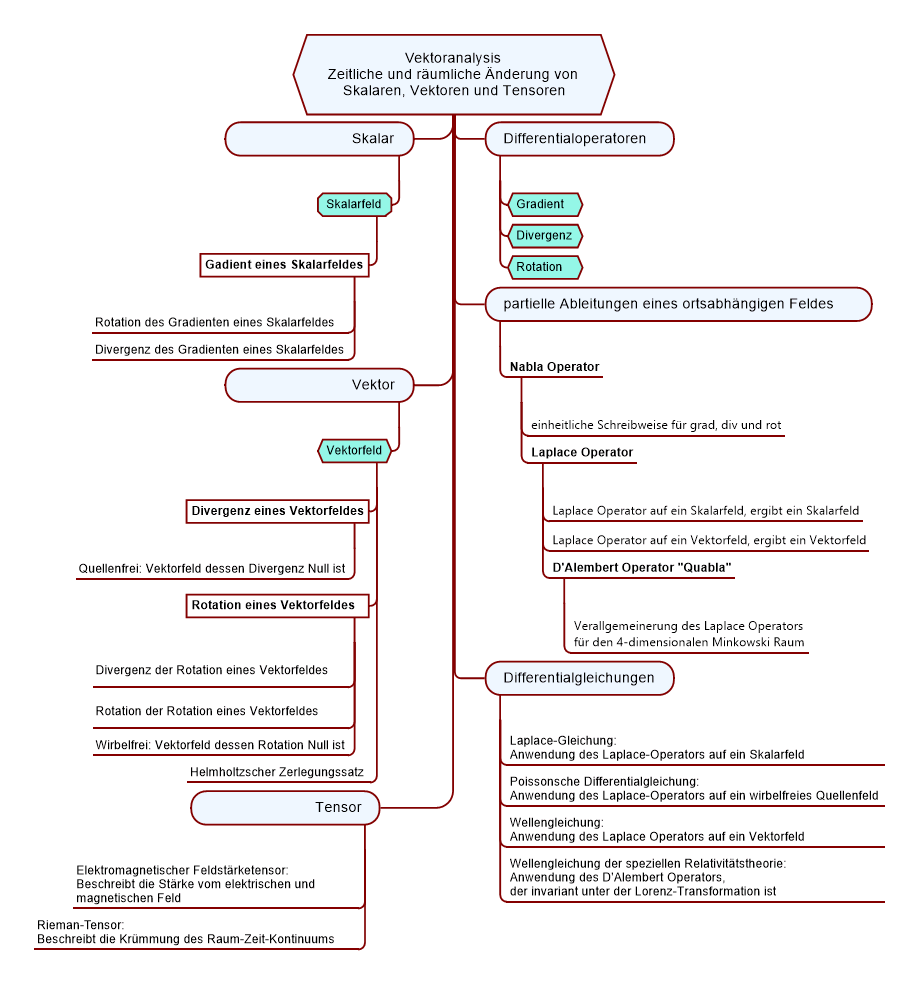
Vektoranalysis

Die Vektoranalysis ist ein Teilgebiet der Mathematik, welches sich mit Skalaren, Vektoren und Tensoren, sowie deren Änderung in Raum und Zeit beschäftigt.

In der Physik spricht man in diesem Zusammenhang von Feldern, z.B.: \(\vec D{\mkern 1mu} - {\mkern 1mu} \vec E{\mkern 1mu} - {\mkern 1mu} \vec B{\mkern 1mu} - {\mkern 1mu} \vec H\) in der Elektrodynamik, in der Mathematik von Funktionen, z.B.: \(\overrightarrow f = \overrightarrow f \left( {x,y,z} \right)\). Die Vektoranalysis verbindet die Vektorrechnung mit der Analysis und dort speziell mit der Infinitesimalrechnung (Differential- und Integralrechnung).

Ein Feld ist eine Energieform, die den Raum erfüllt. Felder können sich mit endlicher Geschwindigkeit ausbreiten, wobei ihre Dynamik durch Feldgleichungen beschrieben wird.

Zeitlich unveränderliche räumliche Felder benötigen zu ihrer Beschreibung eine Funktion mit den 3 Variablen \(\overrightarrow f = \overrightarrow f \left( {x,y,z} \right)\) , um das Feld in jedem Punkt im 3-dimensionalen Raum beschreiben zu können. Will man eine derartige Funktion ableiten, so bedient man sich der partiellen Ableitung. Bei der partiellen Ableitung leitet man jeweils nach einer der unabhängigen Variablen ab, und behandelt die anderen unabhängigen Variablen wie Konstante.

Ein wichtiges Anwendungsgebiet der Vektoranalysis sind elektromagnetische Felder. Die maxwellschen Gleichungen, in Integral- und Differentialform zur Beschreibung des elektromagnetischen Feldes, sind fundamentale Anwendungsgebiete der Vektoranalysis in der physikalischen Praxis.

Ein weiteres wichtiges Anwendungsgebiet der Vektoranalysis sind die 4 fundamentalen Wechselwirkungen, die beschreiben, wie physikalische Objekte einander beeinflussen, samt dem Higgs-Feld, welches dafür sorgt, dass Teilchen ihre Masse erhalten.

Die Verwendung von Tensoren, speziell von Minkowski-Raumzeit-Tensoren ermöglichte eine kompakte Darstellung der Lorentz-Transformation in der speziellen Relativitätstheorie und die Formulierung der Beziehung zwischen der Gravitationskraft einerseits und der Krümmung der Raumzeit andererseits, zufolge der Einstein-Tensorgleichung der allgemeinen Relativitätstheorie.

Felder, durch Tensoren dargestellt

Ein Tensor ist ein mathematischer Begriff zur Verallgemeinerung von Skalaren, Vektoren und Matrizen. Der Rang eines Tensors ergibt sich aus der Anzahl der Indizes, die benötigt werden, um ein Element zu referenzieren.  

Man kann Felder nach ihrem Rang wie folgt unterscheiden:

• Skalarfelder
  Ein Skalarfeld ist ein Tensor des Rangs 0, da es nur einen Wert gibt, und somit kein Index nötig ist.
  • Temperatur im Raum
  • Higgs Feld
• Vektorfelder
  Ein Vektorfeld ist ein Tensor des Rangs 1, da nur 1 Index zur Beschreibung nötig ist.
  • Die elektromagnetischen Felder \(\vec D{\mkern 1mu} - {\mkern 1mu} \vec E{\mkern 1mu} - {\mkern 1mu} \vec B{\mkern 1mu} - {\mkern 1mu} \vec H\) , z.B.: \(\overrightarrow {{E_x}} ,\overrightarrow {{E_y}} ,\overrightarrow {{E_z}} \)
  • Feld der schwachen Wechselwirkung
  • Feld der starken Wechselwirkung
• Tensorfelder
  Matrizen sind Tensor vom Rang >1, da 2 oder mehr Indizes zur Beschreibung der Elemente nötig sind.
  • Elektromagnetischer Feldstärkentensor \({F^{\mu \upsilon }}\) ist ein Tensor des Rangs 2, der sowohl die Stärke des elektrischen Feldes E als auch die Stärke des magnetischen Feldes B umfasst.
  • Riemann-Tensor zur Beschreibung der Krümmung des Raum-Zeit-Kontinuums ist ein Tensor des Rangs 4.

Wir verwenden folgende Schreibweise:

• s steht für ein Skalarfeld, in der Literatur wird auch gerne f verwendet
• \(\overrightarrow v \) steht für ein Vektorfeld, in der Literatur wird auch gerne F verwendet
• T_ij unter Verwendung von fetten Buchstaben und Indizes steht für ein Tensorfeld

Differentialoperatoren

Ein Differentialoperator ist eine Abbildungsvorschrift, bei der einer Ausgangsfunktion eine andere Funktion zugeordnet wird, die partielle Ableitungen der Ausgangsfunktion hat.

So bildet etwa der Differentialoperator \(\dfrac{d}{{dx}}\) eine differenzierbare Funktion \(f\left( x \right)\) auf deren 1. Ableitung ab:

\(f\left( x \right) \to \dfrac{d}{{dx}} \to f'\)

Wir werden nun folgende Differentialoperatoren besprechen:

• Gradient, gibt die Richtung des steilsten Anstiegs des Skalarfeldes in Form eines Vektors an
• Divergenz, ist ein Maß für die Existenz von Quellen oder Senken in einem Vektorfeld
• Rotation, ist ein Maß für Drehbewegungen bzw. für die Wirbel des Vektorfeldes.

Zur Vereinfachung der Schreibweise von partiellen Ableitungen dienen folgende Differentialoperatoren:

• Nabla-Operator, entspricht dann der ersten partiellen Ableitung eines ortsabhängigen Feldes und vereinheitlicht die Schreibweise für Gradient, Divergenz und Rotation
• Laplace-Operator, entspricht dann der zweiten partiellen Ableitung eines ortsabhängigen Feldes.
• D’Alembert-Operator, stellt eine Verallgemeinerung des Laplace Operators für den 4-dimensionalen Minkowski Raum dar und ist invariant unter der Lorentz-Transformation.

Gradient

Der Gradient ist jener Differentialoperator, der einem räumlichen Skalarfeld \(s \to s\left( {x,y,z} \right)\) den Vektor der partiellen Ableitungen des Skalarfeldes zuordnet. Dieser Vektor heißt Gradient und kann mit dem Nabla-Operator einfach angeschrieben werden.

\(grad\,s = \overrightarrow \nabla s = \left( {\begin{array}{*{20}{c}} {{\partial _x}s}\\ {{\partial _y}s}\\ {{\partial _z}s} \end{array}} \right)\)

Umgekehrt formuliert, bildet der Differentialoperator, diesmal als Zeilenvektor geschrieben, \(\left( {\dfrac{\partial }{{\partial x}},\dfrac{\partial }{{\partial y}},\dfrac{\partial }{{\partial z}}} \right)\) ein zeitlich unveränderliches räumliches Skalarfeld \(s = s\left( {x,y,z} \right)\)auf dessen Gradienten – ein Vektorfeld - ab:

\(s\left( {x,y,z} \right) \to \left( {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}}\\ {\dfrac{\partial }{{\partial y}}}\\ {\dfrac{\partial }{{\partial z}}} \end{array}} \right) \to grad\,s = \overrightarrow \nabla \,s\)

Rechenregeln:

\(\begin{array}{l} \overrightarrow \nabla \left( {f + g} \right) = \overrightarrow \nabla f + \overrightarrow \nabla g\\ \overrightarrow \nabla \left( {f \cdot g} \right) = f \cdot \overrightarrow \nabla g + g \cdot \overrightarrow \nabla f \end{array}\)

Beispiel:  Anwendung des Nabla-Operators auf eine Funktion mit 3 unabhängigen Variablen, bzw. Bildung des Gradienten der Funktion

\(\begin{array}{l} s\left( {x,y,z} \right) = {x^2} + {y^2} + {z^2}\\ grad\,s = ?\\ \\ \dfrac{{\partial s}}{{\partial x}} = 2x + 0 + 0\\ \dfrac{{\partial s}}{{\partial y}} = 0 + 2y + 0\\ \dfrac{{\partial s}}{{\partial z}} = 0 + 0 + 2z\\ \\ \overrightarrow \nabla s = grad\,s = \left( {\begin{array}{*{20}{c}} {2x}\\ {2y}\\ {2z} \end{array}} \right) = 2x \cdot \overrightarrow i + 2y \cdot \overrightarrow j + 2z \cdot \overrightarrow k \end{array}\)

mit

\(\overrightarrow i ,\overrightarrow j {\text{ und }}\overrightarrow k {\text{ : Basisvektoren}}\)

Divergenz

Der Divergenz ist jener Differentialoperator, der einem räumlichen Vektorfeld \(\overrightarrow v \to \overrightarrow v \left( {x,y,z} \right)\) die Summe der partiellen Ableitung der x,y,z-Koordinate zuordnet. Diese Summe ist ein Skalar. Sie ist ein Maß für die Quellenstärke des Vektorfeldes in einem bestimmten Punkt. 

Mathematisch ist die Divergenz das Skalarprodukt aus dem Nabla-Vektor und dem räumlichen Vektorfeld.

\(div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v = \sum\limits_{i = x}^z {{\partial _i}{v_i}} = \dfrac{{\partial {v_x}}}{{\partial x}} + \dfrac{{\partial {v_y}}}{{\partial y}} + \dfrac{{\partial {v_z}}}{{\partial z}}\)

Rechenregeln:

\(\begin{array}{l} div\left( {\overrightarrow u + \overrightarrow v } \right) = div\overrightarrow u + div\overrightarrow v \\ div\left( {s \cdot \overrightarrow v } \right) = s \cdot div\overrightarrow v + \left( {\overrightarrow {\nabla s} } \right) \cdot \overrightarrow v \\ div\left( {\overrightarrow u \times \overrightarrow v } \right) = \overrightarrow v \cdot rot\overrightarrow u - \overrightarrow u \cdot rot\overrightarrow v \end{array}\)

Beispiel:  Anwendung des Skalarprodukts aus dem Nabla-Operator und einer Vektorfunktion mit 3 unabhängigen Variablen, bzw. Bildung der Divergenz der Funktion.

\(\begin{array}{l} \overrightarrow v \left( {x,y,z} \right) = \left( {\begin{array}{*{20}{c}} {3xz - 4{e^{2z}}}\\ {2z + 2x{e^{ - 4y}}}\\ {3x{y^2}z} \end{array}} \right)\\ div\,\overrightarrow v = ?\\ \\ div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v \\ NR.:\\ \dfrac{{\partial {v_x}}}{{\partial x}} = \dfrac{d}{{dx}} \cdot \left( {3xz - 4{e^{2z}}} \right) = 3z\\ \dfrac{{\partial {v_y}}}{{\partial y}} = \dfrac{d}{{dy}} \cdot \left( {2z + 2x{e^{ - 4y}}} \right) = - 4 \cdot 4x \cdot {e^{ - 4y}}\\ \dfrac{{\partial {v_z}}}{{\partial z}} = \dfrac{d}{{dz}} \cdot \left( {3x{y^2}z} \right) = 3x{y^2}\\ \\ div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v = \sum\limits_{i = x}^z {{\partial _i}{v_i}} = 3z - 16x \cdot {e^{ - 4y}} + 3x{y^2} \end{array}\)

Setzt man nun für einen Punkt des Vektorfeldes ein, gibt es 3 Möglichkeiten:

\(\eqalign{ & P\left( {{x_P}|{y_P}|{z_p}} \right) \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 > 0 \to {\text{P ist Quelle}} \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 < 0 \to {\text{P ist Senke}} \cr & div\,\overrightarrow v = 3{z_P} - 16{x_P} \cdot {e^{ - 4{y_P}}} + 3{x_P}{y_P}^2 = 0 \to {\text{P ist weder Quelle noch Senke}} \cr} \)

Rotation

Die Rotation ist jener Differentialoperator, der einem räumlichen Vektorfeld \(\overrightarrow v \to \overrightarrow v \left( {x,y,z} \right)\) ein anderes räumliches Vektorfeld gemäß dem Kreuzprodukt aus dem Gradienten des Vektorfeldes und dem Vektorfeld selbst zuordnet.

Mathematisch ist die Rotation das Kreuzprodukt aus dem Nabla-Vektor und dem räumlichen Vektorfeld.

\(rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v = \left( {\dfrac{{\partial {v_z}}}{{\partial y}} - \dfrac{{\partial {v_y}}}{{\partial z}},\dfrac{{\partial {v_x}}}{{\partial z}} - \dfrac{{\partial {v_z}}}{{\partial x}},\dfrac{{\partial {v_y}}}{{\partial x}} - \dfrac{{\partial {v_x}}}{{\partial y}}} \right)\)

Rechenregeln:

\(\begin{array}{l} rot\left( {\overrightarrow u + \overrightarrow v } \right) = rot\overrightarrow u + rot\overrightarrow v \\ rot\left( {s \cdot \overrightarrow v } \right) = s \cdot rot\overrightarrow v + \left( {\overrightarrow \nabla s} \right) \times \overrightarrow v \\ rot\left( {\overrightarrow u \times \overrightarrow v } \right) = \left( {\overrightarrow v \circ \overrightarrow \nabla } \right)\overrightarrow u - \overrightarrow v \left( {\overrightarrow \nabla \circ \overrightarrow u } \right) - \left( {\overrightarrow u \circ \overrightarrow \nabla } \right)\overrightarrow v + \overrightarrow u \left( {\overrightarrow \nabla \circ \overrightarrow v } \right) \end{array}\)

Beispiel:  Anwendung des Kreuzprodukts aus dem Nabla-Operator und einer Vektorfunktion mit 3 unabhängigen Variablen, bzw. Bildung der Divergenz der Funktion.

\(\begin{array}{l} \overrightarrow v \left( {x,y,z} \right) = \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x^2} + {z^3}}\\ {{x^2} + {y^3}}\\ {{y^2} + {z^3}} \end{array}} \right)\\ rot\,\overrightarrow v = ?\\ \\ rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v \\ rot\,\overrightarrow v = \left( {\begin{array}{*{20}{c}} {{\partial _y}{v_z} - {\partial _z}{v_y}}\\ {{\partial _z}{v_x} - {\partial _x}{v_z}}\\ {{\partial _x}{v_y} - {\partial _y}{v_x}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\dfrac{{d\left( {{y^2} + {z^3}} \right)}}{{dy}} - \dfrac{{d\left( {{x^2} + {y^3}} \right)}}{{dz}}}\\ {\dfrac{{d\left( {{x^2} + {z^3}} \right)}}{{dz}} - \dfrac{{d\left( {{y^2} + {z^3}} \right)}}{{dx}}}\\ {\dfrac{{d\left( {{x^2} + {y^3}} \right)}}{{dx}} - \dfrac{{d\left( {{x^2} + {z^3}} \right)}}{{dy}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {2y - 0}\\ {3{z^2} - 0}\\ {2x - 0} \end{array}} \right)\\ \\ rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v = \left( {\begin{array}{*{20}{c}} {2y}\\ {3{z^2}}\\ {2x} \end{array}} \right) \end{array}\)

Das bedeutet, dass sich jeder Punkt des räumlichen Vektorfeldes um die Rotationsachse \(\left( {\begin{array}{*{20}{c}} {2y}\\ {3{z^2}}\\ {2x} \end{array}} \right)\) dreht.

Mit Hilfe der Differentialoperatoren Gradient (grad), Divergenz (div) und Rotation (rot) kann man die Eigenschaften von Feldern untersuchen.

• Wendet man Gradient auf ein skalares Feld an, erhält man ein Vektorfeld.
• Wendet man Divergenz auf ein Vektorfeld an, erhält man ein Skalarfeld.
• Wendet man Rotation auf ein Vektorfeld an, erhält man wieder ein Vektorfeld.

grad, div und rot sind unterschiedliche Arten der Differentiation im Zusammenhang mit der Vektorrechnung.

Zur Vereinfachung der Schreibweise partieller Ableitungen bedient sich die Vektoranalysis weiterer Operatoren

Differentialoperator Nabla

Der Nabla-Operator ist ein vektorieller Differentialoperator und hat alleinstehend keine Bedeutung. Er muss auf ein Skalar s oder einen Vektor \(\overrightarrow v \) angewendet werden und entspricht dann der ersten partiellen Ableitung eines ortsabhängigen Feldes.

Der Nabla-Operator fasst in einem Symbol \(\overrightarrow \nabla \) die drei partiellen Differentiationen nach der jeweiligen Ortskoordinate x, y bzw. z zusammen.

\(\vec \nabla = \left( {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}}\\ {\dfrac{\partial }{{\partial y}}}\\ {\dfrac{\partial }{{\partial z}}} \end{array}} \right)\)

Mit Hilfe vom Differentialoperator Nabla ist es möglich die Operatoren grad, div und rot in einer einheitlichen Form anzuschreiben.

\(\begin{array}{*{20}{l}} {grad\,s = \overrightarrow \nabla s}\\ {div\,\overrightarrow v = \overrightarrow \nabla \circ \overrightarrow v }\\ {rot\,\overrightarrow v = \overrightarrow \nabla \times \overrightarrow v } \end{array}\)

Laplace Operator

Der Laplace Operator ist ein Differentialoperator und hat alleinstehend keine Bedeutung. Er entspricht der zweifachen Anwendung des Nabla Operators. Er muss auf ein Skalar s oder einen Vektor \(\overrightarrow v \) angewendet werden und entspricht dann der zweiten partiellen Ableitung eines jeweiligen ortsabhängigen Feldes.

\(\overrightarrow \nabla \circ \overrightarrow \nabla = {\overrightarrow \nabla ^2} = \Delta {\rm{ }}...{\rm{Laplace Operator}}\)

\({\rm{\Delta }} = \left( {\dfrac{{{\partial ^2}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}}}{{\partial {z^2}}}} \right)\)

Laplace Operator auf ein Skalarfeld angewendet

Wendet man den Laplace Operator auf ein Skalarfeld s an, ist das Resultat wieder ein Skalar.

\({\nabla ^2}s = {\rm{\Delta s}} = \dfrac{{{\partial ^2}s}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}s}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}s}}{{\partial {z^2}}}\)

• Ein Beispiel für die Anwendung des Laplace Operators auf ein Skalarfeld ist die Laplace-Gleichung. Skalarfelder \(s\left( {x,y,z} \right)\) die der Laplacegleichung \({\rm{\Delta s}} = 0 \) genügen, sind quellen- und wirbelfrei, etwa die Temperaturverteilung in einem homogenen Medium.
  \(\begin{array}{*{20}{l}} {\overrightarrow \nabla s = grad{\mkern 1mu} s}\\ {div\,\overrightarrow s = div\left( {grad{\mkern 1mu} {\mkern 1mu} s} \right) = {\rm{\Delta s}} = 0 \to {\rm{Quellenfreiheit}}}\\ {rot\,\overrightarrow s = rot\left( {grad{\mkern 1mu} {\mkern 1mu} s} \right) = 0 \to {\rm{Wirbelfreiheit}}} \end{array}\)

• Ein Beispiel für die Anwendung des Laplace-Operators auf ein wirbelfreies Quellenfeld, etwa das elektrische Potential, ist die poissonsche Differentialgleichung
  \({\nabla ^2}\varphi = {\rm{\Delta }}\varphi = \dfrac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\varphi }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\varphi }}{{\partial {z^2}}} = - q\)
  der zufolge der Laplace-Operator des elektrischen Potentials Phi gleich der negativen Ladungsdichte q ist. Diese Gleichung beschreibt, wie jede punktförmige Ladung Q an einem Punkt im Raum, einen Beitrag zum Potential Phi an einem anderen Punkt im Raum erbringt.

Laplace Operator auf ein Vektorfeld angewendet

Wendet man den Laplace Operator auf ein Vektorfeld \(\overrightarrow v \) an, ist das Resultat wieder ein Vektor.
\({\nabla ^2}\overrightarrow v = {\rm{\Delta }}\overrightarrow v = \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\overrightarrow v }}{{\partial {z^2}}}\)

Ein Beispiel für die Anwendung des Laplace Operators auf ein Vektorfeld ist die Wellengleichung.

Die Wellengleichung beschreibt die Ausbreitung von Wellen in Raum und Zeit mittels einer partiellen Differenzialgleichung. Sie besagt, dass die 2. räumliche Ableitung der Auslenkung proportional zur 2. zeitlichen Ableitung der Auslenkung ist, wobei der Proportionalitätsfaktor 1/c² beträgt. Der Laplace Operator ist eine Kurzschreibweise für die 2. räumliche Ableitung.
\(\begin{array}{l} \psi = \psi \left( {x,y,z,t} \right)\\ \dfrac{{{\partial ^2}\psi }}{{\partial {x^2}}} + \dfrac{{{\partial ^2}\psi }}{{\partial {y^2}}} + \dfrac{{{\partial ^2}\psi }}{{\partial {z^2}}} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}}\\ \Delta \psi = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}}\\ \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}\psi }}{{d{t^2}}} - \Delta \psi = 0 \end{array}\)

D’Alembert-Operator Quabla

Der D’Alembert Operator namens "Quabla", auch als Wellenoperator bezeichnet, ist ein hyperbolischer Differentialoperator. Er ist eine lineare Kombination aus der zeitlichen Ableitung und dem Laplace-Operator.

Er stellt eine Verallgemeinerung des Laplace Operators für den 4-dimensionalen Minkowski Raum dar und findet daher im Rahmen der speziellen Relativitätstheorie (SRT) Anwendung. Der D’Alembert Operator ist invariant unter der Lorentz-Transformation.

\(\square = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - {\Delta} = \dfrac{1}{{{c^2}}} \cdot \dfrac{{{\partial ^2}}}{{\partial {t^2}}} - \dfrac{\partial }{{\partial {x^2}}} - \dfrac{\partial }{{\partial {y^2}}} - \dfrac{\partial }{{\partial {z^2}}}\)

Manche Autoren schreiben obige Gleichung gleichwertig auch wie folgt an

\(\square = {\nabla ^2} - \dfrac{1}{{{c^2}}}\dfrac{{{\partial ^2}}}{{\partial {t^2}}}\)

wobei:

c … Lichtgeschwindigkeit

• Die Wellengleichung in der speziellen Relativitätstheorie mit dem D’Alembert-Operator formuliert lautet: 
  \(\eqalign{ & \psi = \psi \left( {x,y,z,t} \right) \cr & \square \psi = 0 \cr} \)
  Diese Gleichung beschreibt, wie sich Wellen (etwa elektromagnetische Wellen) in der Raumzeit ausbreiten. Sie besagt, dass die Wellenfunktion in allen 4 Raumzeit-Koordinaten (x,y,z und t) glatt ist und keine Divergenz oder Rotation hat.

Skalarfeld

In einem Skalarfeld wird jedem Punkt des vom Feld erfüllten Raums ein bestimmter Absolutwert \({s_P} = s\left( {{P_x},{P_y},{P_z}} \right)\) zugeordnet. 

\(s = s\left( {x,y,z} \right)\)

Beispiele für Skalarfelder sind die Temperatur in einem Raum oder das Potential.

Illustration eines Skalarfeldes

Bild

Gradient eines Skalarfeldes

Das Produkt des Nabla-Operators mit einem Skalarfeld f(x,y,z) nennt man Gradient. Der Gradient ist ein Vektor, dessen x,y,z-Komponenten sich aus den 3 ersten partiellen Ableitung (nach x, nach y, nach z) der Gleichung vom Skalarfeld ergeben.

Der Gradient gibt die Richtung des steilsten Anstiegs des Skalarfeldes in Form eines Vektors an. Der Betrag des Gradienten gibt, wie bei Betrag eines x-beliebigen Vektors, die Größe der Änderung an.

Das Resultat ist ein Vektorfeld. Der Gradient ordnet einem Skalarfeld, welches naturgemäß keine Richtung aber eine Ortsabhängigkeit hat, ein Vektorfeld zu, welches die Richtung der größten Zunahme des Skalarfelds anzeigt.

\(\eqalign{ & \vec \nabla s = \operatorname{grad} s = \left( {\dfrac{{\partial s}}{{\partial x}},\dfrac{{\partial s}}{{\partial y}},\dfrac{{\partial s}}{{\partial z}}} \right) \cr & \left| {\operatorname{grad} s} \right| = \sqrt {{{\left( {\dfrac{{\partial s}}{{\partial x}}} \right)}^2} + {{\left( {\dfrac{{\partial s}}{{\partial y}}} \right)}^2} + {{\left( {\dfrac{{\partial s}}{{\partial z}}} \right)}^2}} \cr} \)

Rechenregeln für Gradienten

\(\eqalign{ & \overrightarrow \nabla \left( {{s_1} + {s_2}} \right) = \overrightarrow \nabla {s_1} + \overrightarrow \nabla {s_2} \cr & \overrightarrow \nabla \left( {{s_1} \cdot {s_2}} \right) = {s_1} \cdot \overrightarrow \nabla {s_2} + {s_2} \cdot \overrightarrow \nabla {s_1} \cr} \)

Der Gradient \(\vec \nabla s = \operatorname{grad} s\) steht senkrecht auf jene Flächen, für die \(s = s\left( {x,y,z} \right) = konst.\) gilt. Wenn die skalare Funktion etwa ein Potential darstellt, bezeichnet man diese Flächen als Äquipotentialflächen und die Richtung der Größten Änderung des Potentials ist senkrecht auf die Äquipotentialfläche.

Illustration vom Gradienten eines Skalarfeldes

Bild

2. Ableitungen von Skalarfeldern

Wendet man Gradient auf ein skalares Feld an, erhält man ein Vektorfeld. Auf dieses Vektorfeld kann man nun die Rotation und die Divergenz anwenden.

Rotation des Gradienten eines Skalarfeldes

Die Rotation des Gradienten eines Skalarfeldes ist Null. Kurz: Skalarfelder sind wirbelfrei.

\({\text{rot}}{\mkern 1mu} {\mkern 1mu} \times {\mkern 1mu} {\mkern 1mu} {\text{grad}}{\mkern 1mu} {\mkern 1mu} s = \overrightarrow \nabla \times \left( {\overrightarrow \nabla s} \right) = 0\)

Divergenz des Gradienten eines Skalarfeldes

Die Divergenz des Gradienten eines Skalarfeldes entspricht der Anwendung vom Laplace-Operator.

\(div\left( {grad{\text{ s}}} \right) = \overrightarrow \nabla \cdot \overrightarrow \nabla s = \Delta s\)

Spezialfall: Ist die Divergenz des Gradienten eines Skalarfeldes null, dann bezeichnet man das Skalarfeld als harmonisch. Bei einem harmonischem Skalarfeld verschwindet in jedem Punkt des Raums die Krümmung des Feldes.

\(div\left( {grad{\text{ s}}} \right) = \overrightarrow \nabla \cdot \overrightarrow \nabla s = \Delta s = 0\)

Beispiel: Harmonisches Skalarfeld

\(\eqalign{ & s\left( {x,y,z} \right) = 2{x^2} - {y^2} - {z^2} \cr & grad{\text{ s = }}\overrightarrow \nabla s = \left( {4x, - 2y, - 2z} \right) \cr & \Delta s = 4 - 2 - 2 = 0 \cr} \)

Vektorfeld

In einem Vektorfeld wird jedem Punkt \(P\left( {{P_x},{P_y},{P_z}} \right)\) des vom Feld erfüllten Raums, ein bestimmter Vektor\(\overrightarrow {{v_P}} = \vec v\left( {{P_x},{P_y},{P_z}} \right)\) zugeordnet.

\(\overrightarrow v = \overrightarrow v \left( {x,y,z} \right)\)

Beispiele für Vektorfelder sind der Wärmefluss oder die elektrische oder magnetische Feldstärke.

Man kann sich ein Vektorfeld räumlich so vorstellen, als würde in jedem Punkt vom Zimmer in dem man sitzt, ein Vektor seinen Anfangspunkt haben. Jeder dieser unendlich vielen Vektoren würde in jene Richtung zeigen, in der sich die Temperatur im Raum am stärksten ändert. Die Länge von jedem der unendlich vielen Vektoren wäre ein Maß dafür, wie stark sich die Temperatur im jeweiligen Raumpunkt ändert. Was wir in den letzten drei Sätzen beschrieben haben, ist das "vektorielle Gradientenfeld vom skalaren Temperaturfeld".

Zu einem Vektorfeld kann man dessen Divergenz (Quellen) und dessen Rotation (Wirbeln) bestimmen. Ein Vektorfeld ist bis auf eine Integrationskonstante eindeutig bestimmt, wenn man dessen Quellen und Wirbel kennt. Die Quellendichte (Divergenz) ist eine skalare Größe, die Wirbeldichte (Rotation) ist eine vektorielle Größe.

Illustration eines Vektorfeldes

Bild

Divergenz eines Vektorfeldes

Das Skalarprodukt vom Nabla-Operator mit einem Vektorfeld \(\overrightarrow v \) nennt man Divergenz. Das Skalarprodukt aus dem Nabla-Vektor und dem Feldvektor ist ein Skalar.

Die Divergenz eines Vektorfeldes ist ein Maß für die Existenz von Quellen oder Senken. Das Resultat ist ein Skalarfeld. Wenn die Divergenz eines Vektorfeldes Null ist, so ist das Vektorfeld quellenfrei.

Elektrische Felder sind ein Beispiel für Quellenfelder, deren Quellen die positiven elektrischen Ladungen und deren Senken die negativen elektrischen Ladungen sind.

\(div\,\vec v = \left( {\dfrac{{\partial {v_x}}}{{\partial x}} + \dfrac{{\partial {v_y}}}{{\partial y}} + \dfrac{{\partial {v_z}}}{{\partial z}}} \right) = \vec \nabla \circ \vec v\)

Die Divergenz eines Vektorfeldes ist ein Skalarfeld, welches für jeden Punkt des Raums angibt, ob dort Feldlinien entstehen, Quelle mit \(div\,\vec v\left( x \right) > 0\) oder verschwinden, Senke mit \(div\,\vec v\left( x \right) < 0\). Die Divergenz ist am Ort einer positiven Punktladung größer null, da dort Feldlinien entstehen.

Rotation eines Vektorfeldes

Das Kreuzprodukt vom Nabla-Operator mit einem Vektorfeld \(\overrightarrow v \) nennt man Rotation. Das Kreuzprodukt aus dem Nabla-Vektor und dem Feldvektor ist ein Vektor. Der Vektor \(rot\overrightarrow v \) bezeichnet die Wirbeldichte des Vektorfeldes \(\overrightarrow v \).

Die Rotation eines Vektorfeldes ist ein Maß für Drehbewegungen bzw. für die Wirbel des Vektorfeldes. Das Resultat ist erneut ein Vektorfeld. Wenn die Rotation eines Vektorfeldes Null ist, so ist das Vektorfeld wirbelfei.

\(rot\,\vec v = \left( {\begin{array}{*{20}{c}} {\dfrac{{\partial {v_z}}}{{\partial y}} - \dfrac{{\partial {v_y}}}{{\partial z}}}\\ {\dfrac{{\partial {v_x}}}{{\partial z}} - \dfrac{{\partial {v_z}}}{{\partial x}}}\\ {\dfrac{{\partial {v_y}}}{{\partial x}} - \dfrac{{\partial {v_x}}}{{\partial y}}} \end{array}} \right) = \vec \nabla \times \vec v\)

Die Rotation eines Vektorfeldes ist ein Vektorfeld, welches angibt, wie stark sich das Vektorfeld \(\overrightarrow v \) n eine bestimmte Koordinatenrichtung ändert. Vektorfelder mit nicht verschwindender Rotation werden Wirbelfelder genannt. Ein Beispiel dafür ist das Magnetfeld.

2. Ableitungen von Vektorfeldern

Divergenz der Rotation eines Vektorfeldes ist immer Null

Der Rotationssatz besagt, dass die Divergenz der Rotation eines Vektorfeldes \(\overrightarrow v \) 

immer Null ist. Das bedeutet, dass die Rotation eines Vektorfeldes nie zu einer Quelle oder Senke führt, oder kurz:

Ein Wirbelfeld ist quellenfrei!
\(div{\mkern 1mu} {\mkern 1mu} rot\,\vec v = \overrightarrow \nabla \circ \left( {\overrightarrow \nabla \times \vec v} \right) = 0\)

Rotation der Rotation eines Vektorfeldes

Die Doppelrotation eines Vektorfeldes ist erneut ein Vektorfeld.

\(rot\,\,rot\overrightarrow v = \overrightarrow \nabla \times \left( {\overrightarrow \nabla \times \overrightarrow v } \right) = \overrightarrow \nabla \left( {\overrightarrow \nabla \circ \overrightarrow v } \right) - \overrightarrow \Delta \circ \overrightarrow v = grad\left( {div\overrightarrow v } \right) - \overrightarrow \Delta \circ \overrightarrow v \)

Fundamentalsatz der Vektoranalysis

• Vektorfelder deren Rotation Null ist, nennt man wirbelfrei.
• Vektorfelder deren Divergenz Null ist, nennt man quellenfrei.

Der Helmholtzsche Zerlegungssatz sagt aus, dass man jedes Vektorfeld \(\overrightarrow v \) als Summe eines wirbelfreien Quellenfeldes \(\overrightarrow {{v_Q}} \) und eines quellenfreien Wirbelfeldes \(\overrightarrow {{v_W}} \) beschreiben kann.

\(\overrightarrow v = \overrightarrow {{v_Q}} + \overrightarrow {{v_W}} \)

Ein allgemeines Vektorfeld ist nur dann eindeutig spezifiziert, wenn sowohl die Quellen- als Wirbeldichten und allfällige Randwerte vorliegen.

Beschriftung im kartesischen Koordinatensystem

Die drei Koordinatenachsen stehen im kartesischen Koordinatensystem orthogonal (in 90°) aufeinander. Die Achsen werden entweder mit x,y und z beschriftet oder mit x₁, x₂, x₃.

Punkt im \({{\Bbb R}^2},\,\,\,{{\Bbb R}^3}\)

Die Lage eines Punkts ist durch den Abstand je Koordinatenrichtung vom Ursprung des Koordinatensystems bestimmt. Abhängig davon, wie die Koordinatenachsen beschriftet wurdenm gibt es unterschiedliche Möglichkeiten Punkte und Vektoren zu beschriften

\(\begin{array}{l} {\Bbb R^{2:}}:P\left( {{P_x}\left| {{P_y}} \right.} \right) \buildrel \wedge \over = P\left( {{P_1}\left| {{P_2}} \right.} \right)\\ {\Bbb R^3}:P\left( {{P_x}\left| {{P_y}\left| {{P_z}} \right.} \right.} \right) \buildrel \wedge \over = P\left( {{P_1}\left| {{P_2}\left| {{P_3}} \right.} \right.} \right) \end{array}\)

Skalar

Skalar ist ein Ausdruck in der Vektorrechnung für eine relle Zahl. Man verwendet den Begriff Skalar um die Richtungsunabhängigkeit einer Größe im Unterschied zum richtungsabhängigen Vektor zu betonen.

Vektor

Ein Vektor ist eine Strecke in der Ebene oder im Raum. Jeder Vektor ist durch Richtung, Orientierung und durch Betrag gekennzeichnet. Vektoren können im Raum beliebig parallelverschoben werden, d.h. ihr Anfangspunkt kann beliebig festgelegt werden, daraus ergibt sich dann ein eindeutiger Endpunkt. Vektoren spielen in der Physik eine große Rolle, so ist etwa die Geschwindigkeit kein Skalar, sondern ein Vektor.

• Geometrisch wird ein Vektor durch einen Pfeil, mit einem Schaft und einer Spitze (definiert die Orientierung) repräsentiert.
• Algebraisch sind Vektoren eindimensionale Listen von Zahlen, wobei die Komponenten des Vektors in Form von Zeilen- und als Spaltenvektor angeschrieben werden können. Die Anzahl der Komponenten eines Vektors stimmt mit der Dimension des Vektors überein. (a_x,a_y,a_z) repräsentiert also einen 3-dimensionalen Vektor. Die Reihenfolge in der die Komponenten angeschrieben werden spielt eine wesentliche Rolle dabei, in welche Richtung der Vektor zeigt

\(\eqalign{ & \overrightarrow a = \overrightarrow {{a_x}} + \overrightarrow {{a_y}} + \overrightarrow {{a_z}} = \left( {\matrix{ {{a_x}} \cr {{a_y}} \cr {{a_z}} \cr } } \right) \cr & \overrightarrow a = {a_x} \cdot \overrightarrow i + {a_y} \cdot \overrightarrow j + {a_z} \cdot \overrightarrow k \cr}\)

Illustration eines Vektors vom Ursprung zum Punkt P

Gegenvektor

Den Gegenvektor erhält man, indem man den Ausgangsvektor um 180° dreht, bzw. indem man den Ausgangsvektor mit dem Skalar -1 multipliziert.  Vektor und Gegenvektor haben den gleichen Betrag, die gleiche Richtung aber entgegengesetzte Orientierung.

\(\overrightarrow a = \left( {\begin{array}{*{20}{c}}
{{a_x}}\\
{{a_y}}\\
{{a_z}}
\end{array}} \right) \Leftrightarrow - \overrightarrow a = - 1 \circ \overrightarrow a = \left( {\begin{array}{*{20}{c}}
{ - {a_x}}\\
{ - {a_y}}\\
{ - {a_z}}
\end{array}} \right)\)

Betrag eines Vektors

Der Betrag bzw. die Länge des Vektors ergeben sich aus dem Abstand zwischen seinem Anfangspunkt, dem Schaft im Punkt "P" und seinem Endpunkt, also seiner Spitze in "Q".

\(\left| {\overrightarrow {PQ} } \right| = \left| {\overrightarrow v } \right| = \sqrt {{{\left( {{Q_x} - {P_x}} \right)}^2} + {{\left( {{Q_y} - {P_y}} \right)}^2} + {{\left( {{Q_z} - {P_z}} \right)}^2}} = \sqrt {{v_x}^2 + {v_y}^2 + {v_z}^2} \)

\(\left| {\overrightarrow v } \right| = \left| {\left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right)} \right| = \sqrt {{v_x}^2 + {v_y}^2 + {v_z}^2} \)

Illustration zur Richtung und zur Berechnung vom Betrag eines zweidimensionalen Vektors

Richtung des Vektors

Die Richtung eins Vektors ist durch seine Lage relativ zu den Achsen des Koordinatensystems bestimmt. Ein Vektor hat eine einzige Richtung! Die Richtung des Vektors kann man aus dem Arkustangens vom Quotienten aus der Differenz der y-Koordinaten und der Differenz der x-Koordinaten zweier Punkte vom Vektor berechnen.

\(\alpha = \arctan \dfrac{{{Q_y} - {P_y}}}{{{Q_x} - {P_x}}}\)

Orientierung eines Vektors

Vektoren mit gleicher Richtung haben entweder gleiche oder entgegengesetzte Orientierung. Die Orientierung wird durch Schaft und Spitze des Vektors definiert. Ein Gegenvektor ist ein Vektor mit gleichem Betrag und gleicher Richtung aber umgekehrter Orientierung als der betrachtete Vektor.

Gleiche Vektoren

Vektoren sind gleich, wenn sie gleich lang, parallel und gleich orientiert (Pfeilspitze) sind. Gleiche Vektoren können unterschiedliche Koordinatendarstellungen haben.

Illustration zur Orientierung, zur Gleichheit von Vektoren und zum Gegenvektor eines Vektors und zu Vektoren mit gleichem Betrag

Nullvektor

Der Nullvektor \(\overrightarrow 0\) hat keine bestimmte Richtung. Seine Länge (sein Betrag) ist null. Der Nullvektor ist das neutrale Element bezüglich der Addition von Vektoren. Schaft und Spitze vom Nullvektor fallen in einem Punkt zusammen.

\(\begin{array}{l} \overrightarrow 0 = \left( {0\left| 0 \right.} \right) = \left( {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right)\\ \overrightarrow {AA} = 0 \end{array}\)

Der Nullvektor ist kollinear zu jedem anderen Vektor und komplanar zu einer von 2 Vektoren aufgespannten Ebene.

Basisvektor

Die Basisvektoren liegen jeweils in einer Koordinatenachse, ihre Länge d.h. ihr Betrag ist 1. Sie spannen das Koordinatensystem auf. Je Dimension gibt es einen eigenen Basisvektor. Seine Komponenten bestehen aus einer "1" und sonst nur aus Nullen.

\(\eqalign{ & \overrightarrow i = \left( {\matrix{ 1 \cr 0 \cr } } \right) \cr & \overrightarrow j = \left( {\matrix{ 0 \cr 1 \cr } } \right) \cr}\)

Einheitsvektor

Der Einheitsvektor \( \overrightarrow {{r_0}}\), hat dieselbe Richtung wie der Richtungs- bzw. der Ortsvektor \( \overrightarrow r\), seine Länge wurde aber auf 1 normiert.

\(\eqalign{ & \overrightarrow {{r_0}} = {{\overrightarrow r } \over {\left| r \right|}} = \left( {\matrix{ {{{{r_x}} \over {\sqrt {{{\left( {{r_x}} \right)}^2} + {{\left( {{r_y}} \right)}^2}} }}} \cr {{{{a_y}} \over {\sqrt {{{\left( {{r_x}} \right)}^2} + {{\left( {{r_y}} \right)}^2}} }}} \cr } } \right) \cr & {\rm{mit}}\,\,\,\left| {\overrightarrow r } \right| \ne 0 \cr}\)

Ortsvektor

Der Ortsvektor ist der Vektor vom Ursprung des Koordinatensystems zu einem gegebenen Punkt. Ein Ortsvektor \(\overrightarrow a\) hat seinen Anfang immer im Ursprung des Koordinatensystems. Seine Richtung, Orientierung und Betrag ergeben sich aus der Lage seines Endpunkts. Einen Ortsvektor darf man daher nicht parallel verschieben, man darf auch nicht seinen Betrag ändern.

\(\overrightarrow a = x.\overrightarrow i + y.\overrightarrow j = \left( {\matrix{ x \cr y \cr } } \right) = \left( {x,y} \right)\)

Verbindungsvektor

Der Verbindungsvektor verbindet zwei Punkte im Raum. Es sind die Punkte P (P_x l P_y) und Q (Q_x l Q_y) gegeben. Der Verbindungsvektor ist jener Vektor, der in P seinen Schaft und in Q seine Spitze hat. Um ihn zu berechnen subtrahiert man vom Ortsvektor zu Q (Spitze) den Ortsvektor zu P (Schaft). Einen Verbindungsvektor darf man daher nicht parallel verschieben, man darf auch nicht seinen Betrag oder seine Orientierung ändern.

In \({{\Bbb R}^2}\):

\(\overrightarrow v = \overrightarrow {PQ} = \overrightarrow {UQ} - \overrightarrow {UP} = Q - P = \left( {\begin{array}{*{20}{c}} {{Q_x} - {P_x}}\\ {{Q_y} - {P_y}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}} \end{array}} \right)\)

In \({{\Bbb R}^3}\):

\(\begin{array}{l} A\left( {{A_x}\left| {{A_y}\left| {{A_z}} \right.} \right.} \right)\\ B\left( {{B_x}\left| {{B_y}\left| {{B_z}} \right.} \right.} \right)\\ \overrightarrow {AB} = B - A = \left( {\begin{array}{*{20}{c}} {{B_x} - {A_x}}\\ {{B_y} - {A_y}}\\ {{B_z} - {A_z}} \end{array}} \right) \end{array}\)

"Spitze minus Schaft Regel": Man erhält den Verbindungsvektor zweier Punkte, indem man Komponentenweise die Koordinaten von der Spitze minus jener vom Schaft anschreibt.

Illustration vom Verbindungsvektor zwischen 2 Punkten

Richtungsvektor als Parallelvektor zum Verbindungsvektor

Der Richtungsvektor \(\overrightarrow r\) ist entweder der Verbindungsvektor oder ein zum Verbindungsvektor paralleler Vektor. Der Richtungsvektor hat zwar eine definierte Länge, aber keine feste Position im Koordinatensystem d.h. er kann parallel verschoben werden und ist noch immer ein Richtungsvektor. Der Verbindungsvektor ist ein besonderer Richtungsvektor, weil sein Anfangs- bzw. Endpunkt mit den besonderen Punkten P und Q zusammenfallen.

Mehrdimensionaler Vektor

Die Anzahl der Komponenten eines Vektors entspricht der Dimension des Raums. Dreidimensionale Vektoren spannen den uns vertrauten dreidimensionalen Raum aus Breite, Tiefe und Höhe auf. Vierdimensionale Vektoren spannen die Raum-Zeit der Physik auf. Bei höherdimensionalen Vektoren nummeriert man die Komponenten, weil die Dimensionen mitunter keinen anschaulichen Namen haben.

\(\eqalign{ & P = \left( {{P_1}\left| {{P_2}\left| {...\left| {{P_n}} \right.} \right.} \right.} \right) \cr & Q = \left( {{Q_1}\left| {{Q_2}\left| {...\left| {{Q_n}} \right.} \right.} \right.} \right) \cr}\)

n-dimensionaler Richtungsvektor von P nach Q:

\(\overrightarrow {PQ} = \left( {\begin{array}{*{20}{c}} {{Q_1} - {P_1}}\\ {{Q_2} - {P_2}}\\ {...}\\ {{Q_n} - {P_n}} \end{array}} \right)\)