Elektromagnetische Felder
Hier findest du folgende Inhalte
Formeln
Elektrisches Potential und Spannung
Bei Anwesenheit von elektrischer Ladung bildet sich ein räumliches elektromagnetisches Feld aus. Ein Feld ist eine Energieform, die den Raum erfüllt. Felder können sich mit endlicher Geschwindigkeit ausbreiten, wobei ihre Dynamik durch Feldgleichungen beschrieben wird. Das elektromagnetische Feld ist ein Vektorfeld. Es gibt in jedem Punkt die coulombsche Kraft nach Größe in Volt pro Meter und Richtung an, die auf eine positive oder negative Ladung ausgeübt wird.
Elektrisches Potential Phi
Das elektrische Potential \(\varphi \) repräsentiert die Fähigkeit eines elektromagnetischen Feldes Arbeit an einer elektrischen Ladung zu verrichten. Wird eine elektrische Ladung auf Grund der coulombschen Kraft durch ein elektromagnetisches Feld bewegt, so wird Arbeit an der Ladung verrichtet wodurch sich ihre potentielle Energie verändert.
\(\varphi = \dfrac{{{W_{pot}}}}{q}\)
| \(\varphi \) | elektrisches Potential mit der Einheit Volt |
| Wpot | potentielle Energie mit der Einheit Joule |
| q | Ladung mit der Einheit Coulomb |
Volt V als Einheit vom elektrischen Potential
Volt V ist die Einheit vom elektrischen Potential \(\varphi \) .
\(1 \cdot V = 1 \cdot \dfrac{J}{C}\)
Elektrisches Potential von einem Bezugspunkt
Irgendwo im Raum wird ein Bezugspunkt mit frei wählbarem Potential \({\varphi _0} = 0V\) festgelegt. Von diesem Bezugspunkt aus kann jedem Punkt im Raum ein bestimmtes Potential \({\varphi _P}\) zugewiesen werden. Das elektrische Potential stellt ein Skalarfeld dar, dessen Einheit das Volt ist. Voraussetzung für das elektrische Potential ist die Wegunabhängigkeit der elektrischen Spannung.
Spannung als Potentialdifferenz
Die Spannung zwischen zwei Punkten P und Q ist nichts anderes, als die Differenz der Potentialwerte der beiden Punkte.
\({U_{PQ}} = {\varphi _P} - {\varphi _Q}\)
Spannung im Bereich konstanten Potentials
Liegt zwischen 2 Punkten P und Q keine elektrische Spannung an, dann handelt es sich um Bereiche konstanten Potentials (Äquipotentialfläche)
\({U_{PQ}} = {\varphi _P} - {\varphi _Q} = 0\)
Spannung gegenüber einem Nullpunkt
In der Elektrotechnik sind die Erde, der Neutralleiter und der Sternpunkt eines entsprechenden Trafos übliche Null- bzw. Bezugspunkte zur Spannungsmessung. Diese Wahl ist auch für die Dimensionierung der Isolation sehr wichtig.
Die Spannung gibt dann den Potentialunterschied zwischen dem Bezugspunkt P und dem Nullpunkt an:
\(\eqalign{ & {U_{0P}} = {\varphi _P} - {\varphi _0} \cr & {\text{sinnvolle Wahl: }}{\varphi _0} = 0 \cr} \)
\({U_{0P}} = {\varphi _P}\)
Illustration von Potentialdifferenzen in einem elektrischen Gleichstromkreis
Volt V als Einheit der elektrischen Spannung
Volt V ist die Einheit der elektrischen Spannung U. 1 Volt ist jene Spannung zwischen zwei Klemmen eines Stromkreises, bei der eine Leistung von 1 Watt bei einer Stromstärke von 1 A umgesetzt wird.
Elektrische Spannung U
Die elektrische Spannung ist der Quotient aus der zur Verschiebung einer Ladung Q erforderlichen elektrischen Arbeit W entlang des Weges von P nach Q und der verschobenen Ladung Q
\({U_{PQ}} = \dfrac{{{W_{PQ}}}}{Q}\)
Elektrische Spannung als Linienintegral der elektrischen Feldstärke
Die Spannung U zwischen den Punkten P und Q ist als das Linienintegral der elektrischen Feldestärke \(\overrightarrow E\) entlang einem beliebigen Weg zwischen P und Q definiert.
\(U = \int\limits_P^Q {\overrightarrow E } \,\,d\overrightarrow s \)
→ Auf die Eigenschaften von Spannung im Gleichstromkreis U bzw. Wechselstromkreis u(t) gehen wir in den diesbezüglichen Kapiteln ausführlich ein
Schon den nächsten Badeurlaub geplant?
Auf maths2mind kostenlos auf Prüfungen vorbereiten!
Damit niemand mehr bei Mathe in's Schwimmen kommt!

Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit
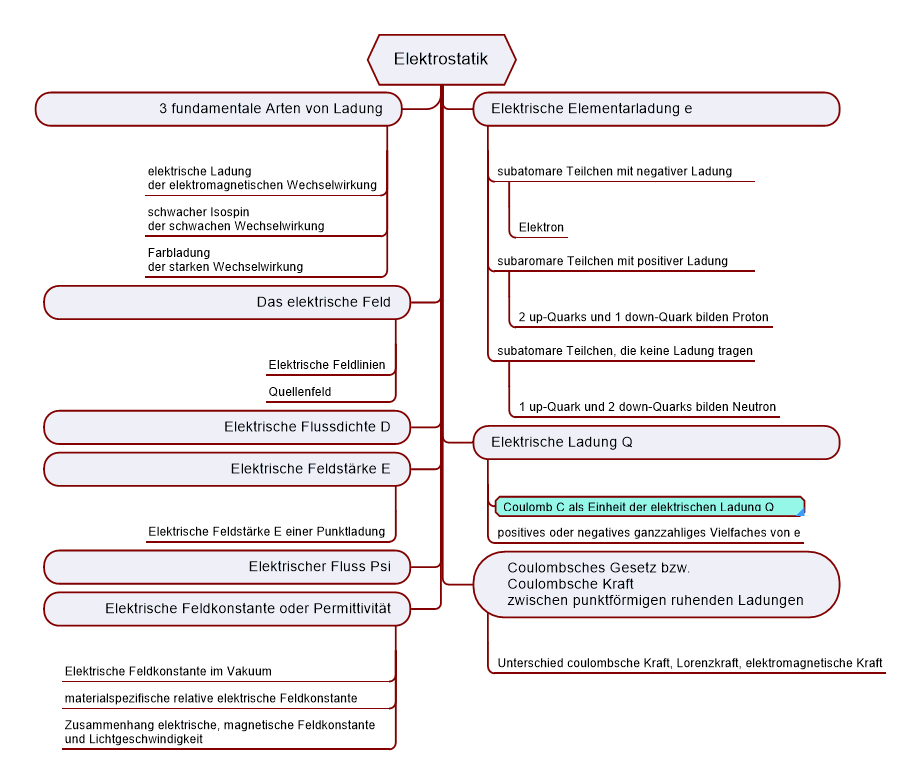
Elektrostatik
Die Elektrostatik ist der einfachste Fall der Elektrodynamik. Sie beschreibt die Felder, die von ruhenden elektrischen Ladungen ausgehen, sowie die Kräfte, die zwischen ruhenden elektrischen Ladungen wirken.
Drei fundamentale Arten von Ladung
Gemäß dem Standardmodell der Elementarteilchen ist Ladung eine fundamentale Eigenschaft von Teilchen. Zusammen mit der Masse des Teilchens, bestimmen die 3 Arten von Ladung, welcher der 4 Wechselwirkungen ein Teilchen unterliegt. Alle drei Arten von Ladungen treten quantisiert auf, d.h. sie können nur bestimmte, diskrete Werte annehmen. Die Ladung eines zusammengesetzten Teilchens, z.B. eines Atoms, setzt sich aus der Summe der Ladungen seiner Einzelteilchen (Elektronen, Quarks) zusammen. Die Summe der Ladung aller Teilchen eines Systems bleibt über alle ablaufenden Prozesse hinweg erhalten.
Es gibt 3 fundamentale Arten von Ladung, die bestimmen welcher Wechselwirkung ein Teilchen unterliegt:
- die elektrische Ladung der elektromagnetischen Wechselwirkung
- den schwachen Isospin der schwachen Wechselwirkung
- die Farbladung der starken Wechselwirkung
- zur vierten Wechselwirkung, der Gravitation, gibt es keine Ladung, die Masse hat aber eine vergleichbare Bedeutung, sie unterliegt aber (noch) nicht der Quantentheorie
- es gibt keine magnetische Ladung, somit keine magnetische Monopole
Elektrische Elementarladung e
Elektrische Elementarladung → Elektrostatik; Elementarmagnetismus → Magnetostatik;
Die Elementarladung ist eine fundamentale Eigenschaft von elektrisch geladenen Teilchen und Ausgangspunkt der Elektrostatik. "Fundamentale" Eigenschaft bedeutet, dass die elektrische Ladung durch keine andere physikalische Größe erklärbar ist. Die Elementarladung ist daher eine Naturkonstante, deren Wert exakt \(e = 1,602\,176\,634 \cdot {10^{ - 19}}C\) beträgt. Das Coulomb ist also die Einheit der elektrischen Elementarladung.
Folgende subatomaren Teilchen tragen negative elektrische Ladung:
- Elektronen: -1e
- Myonen: -1e
- Tauonen: -1e
- down-Quark: -1/3 e
- strange Quark: -1/3 e
- bottom-Quark: -1/3 e
Folgende subatomaren Teilchen tragen positive elektrische Ladung:
- up-Quark: +2/3 e
- charm Quark: +2/3 e
- top-Quark: +2/3 e
Nicht alle subatomaren Teilchen tragen Ladung.
- Elektron-Neutrino, Myon-Neutrino, Tau-Neutrino, Photonen, ... sind keine Träger elektrischer Elementarladung
Die elektrische Ladung des Protons ist exakt gleich groß wie die elektrische Ladung des Elektrons. Die Ladung des Protons ist positiv, die Ladung des Elektrons ist negativ. Die beiden Ladungen sind einander entgegengesetzt. Das Neutron ist elektrisch neutral, also nicht geladen.
Während das Elektron fundamental, also unteilbar ist, setzt sich das Proton und das Neutron seinerseits aus 3 ihrerseits fundamentalen Quarks zusammen, welche die eigentlichen Träger der elektrischen Ladung im Proton bzw. Neutron sind. Quarks können aber auf Grund eines quantenmechanischen Effekts, der „Confinement“ genannt wird, nicht allein sondern nur als Zusammensetzung aus 2, 3 oder 5 Quarks existieren. Lediglich Protonen und im Atomkern gebundene Neutronen sind stabil.
- Das Elektron ist fundamental, also aus keinen weiteren subatomaren Teilchen aufgebaut. Es ist mit -e negativ geladen.
- Ein Proton besteht aus zwei up-Quarks (+2/3) und einem down-Quark (-1/3). Es ist positiv geladen. Für die elektrische Ladung des Protons ergibt sich:
\(\left( {2 \cdot \dfrac{2}{3} - \dfrac{1}{3}} \right) \cdot e = \dfrac{{4 - 1}}{3} \cdot e = e\)
- Ein Neutron besteht aus einem up-Quark (+2/3) und zwei down-Quarks (-1/3) . Es ist elektrisch neutral. Für die elektrische Ladung des Neutrons ergibt sich:
\(\left( {\dfrac{2}{3} - 2 \cdot \dfrac{1}{3}} \right) \cdot e = \dfrac{{2 - 2}}{3} \cdot e = 0\)
Elektrische Ladung Q
Elektrische Ladung → Elektrostatik; Polstärke → Magnetostatik;
Die elektrische Ladung Q ist immer ein ganzzahliges, positives oder negatives Vielfaches der Elementarladung e. Die elektrische Ladung Q ist also die Summe der Elementarladungen e. Das Coulomb ist also die Einheit der elektrischen Ladung.
\(\eqalign{ & Q = n \cdot e{\text{ mit n}} \in {\Bbb Z}{\text{ (Menge der ganzen Zahlen)}} \cr & {\text{Q = }}{{\text{Q}}_ + } + {Q_ - } \cr} \)
Wobei Q+ für Protonen und Q- für Elektronen steht.
Alle Ladungen Q sind von einem elektrischen Feld \(\overrightarrow E \) umgeben. Die elektrische Ladung verändert nämlich den umgebenden Raum, indem sie dort ein elektrisches Feld erzeugt.
Coulomb C
Coulomb → Elektrostatik; Weber → Magnetostatik;
Das Coulomb C ist die Einheit der elektrischen Ladung. 1 Coulomb ist jene elektrische Ladung, die innerhalb von einer Sekunde durch den Querschnitt eines Leiters transportiert wird, in dem ein Strom von 1 Ampere fließt.
Die Einheit der Ladung Q ergibt sich gemäß folgender Einheitengleichung
\(\left[ Q \right] = \left[ I \right] \cdot \left[ t \right] = A \cdot s = C = \dfrac{{Nm}}{V}\)
Wenn elektrischer Strom fließt, bewegen sich elektrische Ladungsträger
\(\eqalign{ & 1{\text{C}} = 1{\text{A}} \cdot 1{\text{s}} \cr & {\text{Q = n}} \cdot {\text{e}} \cr & {\text{n = }}\dfrac{Q}{e} = \dfrac{{1\operatorname{C} }}{{1,602{\mkern 1mu} 176{\mkern 1mu} 634 \cdot {{10}^{ - 19}}C}} \approx 6,2415 \cdot {10^{18}} \cr} \)
Damit ein Strom von 1A für die Dauer von 1 Sekunde fließt, müssen sich in dieser Zeitspanne 6,2 Trillionen Elektronen durch den Leiterquerschnitt bewegen.
Bei Gleichstrom bewegen sich die Elektronen physikalisch vom Minus- zum Pluspol, bei Wechselstrom schwingen die Elektronen im Leiter abhängig von der Frequenz hin und her, ohne sich makroskopisch über die Amplitude der Schwingung hinaus zu bewegen.
Coulombsche Kraft zwischen zwei punktförmigen ruhenden Ladungen
Coulombsches Gesetz → Elektrostatik; Magnetisches Kraftgesetz → Magnetostatik;
Das Coulombsche Gesetz stellt einen Zusammenhang zwischen den elektrischen Größen „Ladung bzw. elektrisches Feld“ und der mechanischen Größe „Kraft“ her. Es ist daher die Basis für den Bau von elektrischen Maschinen.
Mit dem coulombschen Gesetz kann die Kraft zwischen 2 punktförmigen ruhenden Ladungen berechnet werden. Die Kraft die 2 punktförmige Ladungen im Vakuum auf einander ausüben, ist indirekt proportional zum Quadrat des Abstands der beiden Ladungen und direkt proportional zum Produkt der beiden Ladungen. Umgekehrt formuliert nimmt die Kraftwirkung sehr rasch, nämlich quadratisch mit der Entfernung, ab.
Das coulombsche Gesetz gilt für gleich- und ungleichnamige Ladungen. Gleichnamige Ladungen stoßen einander ab, ungleichnamige Ladungen ziehen einander an.
\({F_{12}} = k \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}} = \dfrac{1}{{4\pi \varepsilon_r {\varepsilon _0}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}}\)
mit \(\varepsilon = {\varepsilon _0} \cdot {\varepsilon _r}\) und der Coulomb-Konstante \(k = 8,99 \cdot {10^9}\dfrac{{{\text{Vm}}}}{{{\text{As}}}}\)
Beispiel: Überprüfen wir das Coulombsche Gesetz mittels einer Einheitengleichung:
\(\begin{array}{l} {F_C} = \dfrac{1}{{4\pi \cdot {\varepsilon _0} \cdot {\varepsilon _r}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{r^2}}}\\ N = \dfrac{1}{{\dfrac{{As}}{{Vm}}}} \cdot \dfrac{{{C^2}}}{{{m^2}}} = \dfrac{{Vm \cdot {C^2}}}{{As \cdot {m^2}}} = \dfrac{{V \cdot {C^2}}}{{As \cdot m}} = \\ {\rm{mit }}C = As = \dfrac{{Nm}}{V} \to V = \dfrac{{Nm}}{C}\\ = \dfrac{{\dfrac{{Nm}}{C} \cdot {C^2}}}{{C \cdot m}} = \dfrac{{Nm \cdot C}}{{C \cdot m}} = N\,\,\,\,{\rm{wzbw}}{\rm{.}} \end{array}\)
Das coulombsche Gesetz gibt ein Maß / eine Formel für jene Kraft an, die 2 punktförmige Ladungen im Vakuum auf einander ausüben und zwar zufolge der fundamentalen elektromagnetischen Wechselwirkung. Der Raum um und zwischen den beiden Ladungen ist von einem elektromagnetischen Feld erfüllt. Das elektrische Feld ist eine Folge des Vorhandenseins von elektrischer Ladung (und einer allfällig zusätzlich vorhandenen zeitlichen Änderung eines Magnetfeldes).
Das Quant / das Boson der fundamentalen elektromagnetischen Wechselwirkung ist das Photon, welches daher der Vermittler der anziehenden oder abstoßenden Kräfte zwischen den beiden punktförmigen Ladungen ist.
Unterschied coulombsche Kraft, Lorentzkraft und elektromagnetische Kraft bzw. Urspannung
Man unterscheidet 3 Arten von Kräften, die auf elektrische Ladungen wirken
- Die coulombsche Kraft wirkt zwischen 2 punktförmigen ruhenden Ladungen, ihre Ursache ist das elektrische Feld. Sie ist daher ein Phänomen der Elektrostatik und bewirkt Spannung zufolge von Potentialunterschieden.
- Die elektromagnetische Kraft (EMK) entspricht der Fähigkeit eines Systems eine Spannung – die „Urspannung“ - zu erzeugen. Konkret ist die Urspannung jene Spannung, die in einem elektrischen Leiter induziert wird, wenn sich der magnetische Fluss durch den Leiter ändert. Es handelt sich dabei um ein Phänomen der Elektrodynamik.
- Die Lorentzkraft wirkt auf bewegte Ladungen im Magnetfeld und ist daher ein Phänomen der Elektrodynamik. Diese Kraft wirkt senkrecht zur Bewegungsrichtung des geladenen Teilchens und senkrecht zur Richtung vom Magnetfeld. Die Lorentzkraft führt dazu, dass sich Elektronen in einem Magnetfeld auf gekrümmten Bahnen bewegen.
Das elektrische Feld
Elektrisches Feld → Elektrostatik; Magnetisches Feld → Magnetostatik;
Sind in einem Raum ruhende oder bewegte elektrische Ladungen Q vorhanden, so verursachen diese Ladungen die Ausbildung eines elektrischen Feldes \(\overrightarrow E \). Zufolge des elektrischen Feldes wirken zwischen gleichnamigen oder ungleichnamigen Ladungen die abstoßende oder anziehende Coulombsche Kraft \(\overrightarrow {{F_C}} \)
Elektrische Feldlinien
Elektrische Feldlinien → Elektrostatik; Magnetische Feldlinien → Magnetostatik;
Alle Ladungen Q sind von einem elektrischen Feld \(\overrightarrow E \) umgeben. Die elektrische Ladung verändert nämlich den umgebenden Raum, indem sie dort ein elektrisches Feld erzeugt.
Elektrische Feldlinien zeigen den Verlauf des Feldes, wobei sie bei positiven Ladungen beginnen und bei negativen Ladungen enden, sich nie schneiden und senkrecht zu den Ladungen stehen. Man spricht daher von einem Quellenfeld. Die positiven Ladungen sind dabei die Quellen, die negativen Ladungen sind die Senken.
Die Dichte der Feldlinien (also wie eng oder weit die Feldlinien auseinander liegen) ist ein Maß für die Feldstärke. Die Feldstärke ist nahe einer Ladung hoch, entsprechend liegen die Feldlinien dicht beieinander und dünnt dann mit zunehmender Entfernung aus. Die Richtung der Coulombschen Kraft auf eine Ladung im Feld wirkt tangential zu den Feldlinien. In einem homogenen Feld liegen die Feldlinien parallel zueinander.
Elektrische Feldstärke
Elektrische Feldstärke → Elektrostatik; Magnetische Feldstärke → Magnetostatik;
Die elektrische Feldstärke \(\overrightarrow E \) ist eine vektorielle Größe, welche die Stärke und die Richtung eines elektrischen Feldes und somit die Fähigkeit des elektrischen Feldes, eine Kraft auf eine darin enthaltene Ladung auszuüben, angibt. Die elektrische Feldstärke entspricht der auf die Längeneinheit der Feldlinie bezogenen Potentialdifferenz. Ihre Ursache sind elektrische Ladungen. Ihre Einheit ist entsprechend Volt pro Meter \(\left[ E \right] = \dfrac{{\text{V}}}{{\text{m}}}\). Die elektrische Feldstärke ist von der Potentialdifferenz, somit also der Spannung (in Volt) und dem Abstand der geladenen Körper (in Meter) abhängig.
\(\vec E = - \dfrac{{\Delta \varphi }}{{\Delta l}}\)
Zwischen zwei benachbarten Potentialflächen muss stets der konstante Potentialwert \(\vartriangle \varphi \) liegen, das bedeutet jedoch noch lange nicht, dass die Potentialflächen auch immer gleich weit voneinander entfernt liegen. Um anzeigen zu können, wo Potentialflächen näher und wo sie weiter voneinander entfernt liegen, wurde die elektrische Feldstärke \(\overrightarrow E \) definiert. Vereinfacht ausgedrückt gibt sie an, wie viele Potentialflächen gerichtet durchstoßen werden, wenn wir in eine bestimmte Richtung um die Wegstrecke \(\Delta l\) weit gehen.
Elektrische Feldstärke einer Punktladung
Die elektrische Feldstärke, die durch eine endliche punktförmig idealisierte Ladung Q ausgeht, nimmt mit dem Quadrat der Entfernung ab. Die Feldlinien stehen radial auf die kugelförmig gedachte Punktladung, die kugelschichtförmig von Äquipotentialflächen umgeben ist.
Die elektrische Feldstärke einer Punktladung Q verläuft radialsymmetrisch. Ihre Stärke nimmt mit 1/r² mit zunehmender Entfernung gemäß folgender Gleichung ab:
\(\left| {\vec E} \right| = \dfrac{1}{{4 \cdot \pi \cdot {\varepsilon _0} \cdot {\varepsilon _r}}} \cdot \dfrac{Q}{{{r^2}}}\)
mit Q als punktförmige Ladung in Coulomb, etwa ein Elektron oder Proton, r als Abstand von der punktförmigen Ladung und \({\varepsilon _0},\,\,{\varepsilon _r}\) als der elektrische Feldkonstante, einer Naturkonstante bzw. Materialkonstante für den vom Feld erfüllten Raum.
Elektrische Flussdichte
Elektrische Flussdichte → Elektrostatik; Magnetische Flussdichte → Magnetostatik;
Die elektrische Flussdichte \(\overrightarrow D \) ist ein vektorielles Maß für die Dichte der elektrischen Feldlinien in Relation zu einer Fläche. Die elektrische Feldstärke \(\overrightarrow E \) ist mit der elektrischen Flussdichte \(\overrightarrow D \) über die elektrische Feldkonstante \(\varepsilon \) verknüpft.
\(\eqalign{ & \overrightarrow D = {\varepsilon _r} \cdot {\varepsilon _0} \cdot \overrightarrow E \cr & \left[ {\overrightarrow D } \right] = \dfrac{{\text{C}}}{{{{\text{m}}^{\text{2}}}}} \cr} \)
Elektrischer Fluss Psi
Elektrische Fluss → Elektrostatik; Magnetische Fluss → Magnetostatik;
Allgemein bezeichnet man jedes Flächenintegral über eine Vektorgröße als Fluss.
Der elektrische Fluss \(\Psi \) (sprich "Psi") ist ein Maß für die Anzahl der elektrischen Feldlinien, die durch ein Flächenelement laufen.
\(\Psi = \iint {\vec D}{\mkern 1mu} {\mkern 1mu} d\vec A = \oint {\vec D{\mkern 1mu} {\mkern 1mu} d\vec A} \)
Zusammenhang elektrische Feldkonstante, magnetische Feldkonstante und Lichtgeschwindigkeit
Die Lichtgeschwindigkeit verknüpft die elektrischer Feldkonstante und magnetischer Feldkonstante wie folgt:
\({c_0} = \dfrac{1}{{\sqrt {{\varepsilon _0} \cdot {\mu _0}} }}\)
Elektrische Feldkonstante (Permittivität)
Elektrische Feldkonstante → Elektrostatik; Magnetische Feldkonstante → Magnetostatik;
Unterschiedliche Materialien haben eine unterschiedliche Durchlässigkeit für elektrische Felder. Das Maß dafür ist die elektrische Feldkonstante bzw. Permittivität \(\varepsilon \) (bzw. veraltet Dielektrizitätskonstante). Die elektrische Durchlässigkeit eines Stoffs \(\varepsilon \) (sprich "Epsilon"), ist das Produkt aus der elektrischen Feldkonstante die im Vakuum \({\varepsilon _0}\) gilt und einem materialspezifischen dimensionslosen Faktor \({\varepsilon _r}\).
\(\begin{array}{l} \varepsilon = {\varepsilon _0} \cdot {\varepsilon _r}\\ \left[ {{\varepsilon _0}} \right] = \left[ \varepsilon \right] = \frac{{As}}{{Vm}}\\ \left[ {{\varepsilon _r}} \right] = 1\\ {\varepsilon _0} = \dfrac{1}{{{c^2} \cdot {\mu _0}}} = 4 \cdot \pi \cdot {10^{ - 7}}\dfrac{{As}}{{Vm}} \end{array}\)
Für das Vakuum gilt:
\({\varepsilon _0} = 8,8542 \cdot {10^{12}}\dfrac{{{\text{As}}}}{{{\text{Vm}}}} = 8,8542 \cdot {10^{12}}\dfrac{F}{m}\)
Da sich Luft nur geringfügig polarisieren lässt, gilt für Luft: \({\varepsilon _r} \approx 1\). Wasser hat eine relative Permittivität von \({\varepsilon _r} \approx 80\). Mit steigender Temperatur nimmt die relative Permittivität ab, was auf die steigende Unordnung der Ladungsträger zurückzuführen ist.
Die relative Permittivität \({\varepsilon _r}\) von Dielektrika ist > 1, jene vom Vakuum ist exakt 1, jene von Leiter ist <1. Die relative Permittivität ist mitunter stark frequenzabhängig.
Vorab eine Mindmap zu den Inhalten dieser Mikro-Lerneinheit
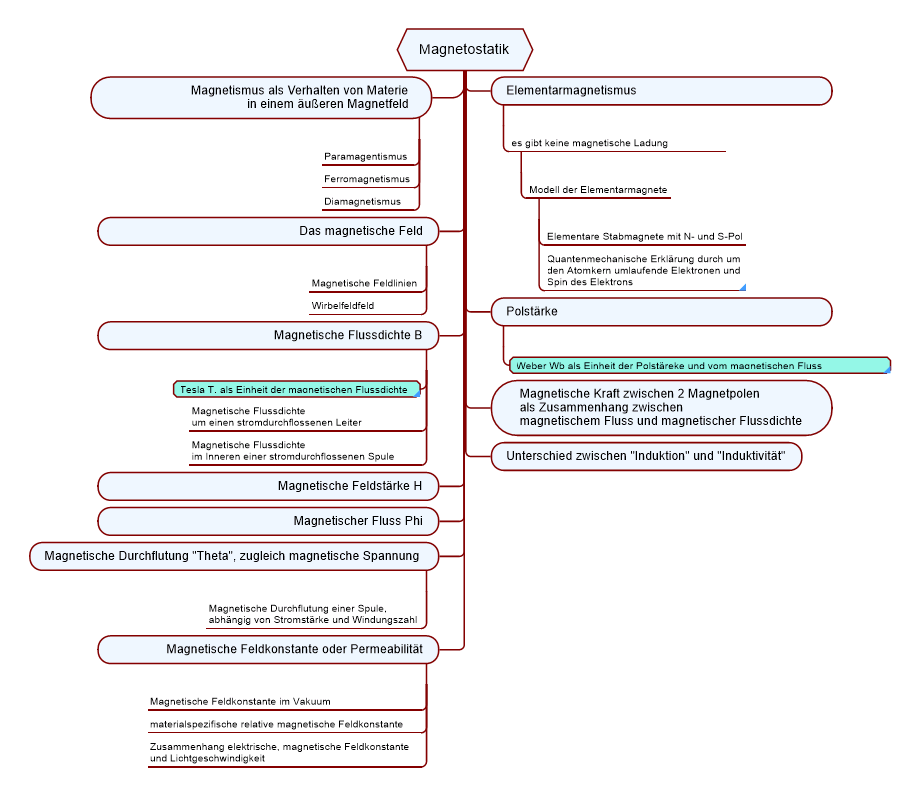
Magnetostatik
Die Magnetostatik ist der einfachste Fall der Elektrodynamik. Sie beschreibt die Felder, die einen von einem zeitunabhängigen Strom (=Gleichstrom) durchflossenen Leiter umgeben, sowie die Kräfte, die zwischen Magnetpolen wirken.
Elementarmagnetismus
Elementarmagnetismus → Magnetostatik; Elektrische Elementarladung → Elektrostatik;
In der Natur gibt zwar die elektrische Elementarladung e aber es gibt keine „magnetische Ladung“. Daher gibt es auch keine magnetischen Monopole, das wären isoliert existierende Nord- oder Südpole. Magnetisch Felder besitzen somit im Unterschied zu elektrischen Feldern keine Quellen (Anfang einer Feldlinie) bzw. Senken (Ende einer Feldlinie), sondern sie sind Wirbelfelder, mit geschlossenen oder sich ins Unedliche windenden Feldlinien. Daher lautet in der Elektrodynamik die 2. Maxwellgleichung, also das Gaußsche Gesetz für magnetische Felder \(div\overrightarrow B = 0\)
Um die magnetischen Eigenschaften von Materie zu erklären verwendet man das Modell der „Elementarmagnete“. Elementarmagnete sind die kleinste magnetische Einheit in einem ferromagnetischen Material. Jedes Atom kann als kleinster isolierbarer Elementarmagnet betrachtet werden, da es ein magnetisches Moment besitzt, welches durch die in der Elektronenhülle umlaufenden und sich dabei drehenden (Spin) Elektronen verursacht werden. Umlaufende Elektronen entsprechen einem Stromfluss, jeder fließende Strom erzeugt ein Magnetfeld.
- Elementare Stabmagnete (als einfache Erklärung): Vereinfacht kann man sich einen Magneten als Ansammlung von elementaren Stabmagneten vorstellen. Jeder Elementarmagnet besitzt einen N-Pol und einen S-Pol und ist frei drehbar. Die Anordnung hängt vom Kristallgitter ab. Bei ferromagnetischen Stoffen führt die gegenseitige Wechselwirkung zu einer Ausrichtung aller Elementarmagnete innerhalb eines sogenannten Weiss’schen Bezirks in die gleiche Richtung.
Ob das magnetische Moment der einzelnen Atome (Elementarmagnete) sich lokal aufhebt oder makroskopisch wirksam wird, hängt von der jeweiligen Anordnung der Atome in der betrachteten Kristallstruktur ab. - Quantenmechanische Erklärung: Wenn - gedanklich - die negativ geladenen Elektronen um den Atomkern umlaufen, so entspricht dies einem Stromfluss um den Kern, der die Ursache für ein Magnetfeld ist. Auch durch die - gedankliche - Eigendrehung des Elektrons (Spin) entsteht ein Beitrag zum magnetischen Dipolmoment.
Ob ein Atom auf Grund der Bahnbewegung und durch den Spin der Elektronen ein magnetisches Moment besitzt, hängt von der Anzahl der Elektronen im Atom und somit vom jeweiligen chemischen Element ab.
Magnetismus als Verhalten von Materie in einem äußeren Magnetfeld
Paramagnetismus
Man spricht vom „Paramagnetismus“ wenn sich die Elementarmagnete unter der Wirkung eines äußeren Magnetfelds so ausrichten, dass sie dieses verstärken. Die Magnetisierung ist dabei proportional zum angelegten Magnetfeld. Paramagnetische Stoffe werden durch ein äußeres Magnetfeld schwach angezogen.
Ferromagnetismus
Von „Ferromagnetismus“ spricht man, wenn sich in kleinen Bereichen des Körpers - in den „Weiß’schen Bezirken“ - die Spins auch ohne äußeres Magnetfeld parallel ausrichten. Da die Spinns benachbarter Bezirke verschieden orientiert sind, hat der Ferromagnet keine makroskopische Magnetisierung. Ferromagnetische Stoffe (bei Raumtemperatur: Eisen, Nickel und Kobalt) werden vom äußeren Magnetfeld stark angezogen. Bei hohen Temperaturen werden ferromagnetische Stoffe paramagnetisch.
Ferromagnetische Stoffe können Magnete bilden, etwa kostengünstige Ferrit Magnete aus Eisenoxid. Sie sind aber nur in Form von Legierungen (z.B.: NdFeB – Neodym, AlNiCo – Aluminium + Nickel + Kobalt, SmCo – Samarium-Kobalt) als Dauermagnete geeignet.
Diamagnetismus
Von „Diamagnetismus“ spricht man, wenn ein äußeres magnetischen Feld \( \overrightarrow H\) auf Materie wirkt, und in jedem Atom ein Kreisstrom induziert wird, dessen magnetisches Moment gemäß der Lenz’schen Regel, dem von außen angelegten Feld entgegengesetzt ist. Diamagnetische Stoffe werden vom äußeren Magnetfeld schwach abgestoßen.
Polstärke
Polstärke → Magnetostatik; Elektrische Ladung → Elektrostatik;
So wie es in der Elektrostatik positive +e und negative Ladungen -e gibt, wo einander gleichnamige Ladungen abstoßen, während sich ungleichnamige Ladungen anziehen, gibt es in der Magnetostatik zwei verschiedene Pole, den Nordpol und den Südpol, wo einander gleichnamige Magnetpole abstoßen, während sich ungleichnamige Magnetpole anziehen. Während man positive und negative elektrische Ladungen trennen kann, kann man Nord- und Südpol eines Magneten nicht trennen. Jeder noch so kleine Magnet hat grundsätzlich immer sowohl N- als auch S-Pol. Man könnte daher formulieren, dass die Polstärke die „scheinbare“ magnetische Ladung eines Magnetpols angibt. Tatsächlich wird sie durch den magnetischen Fluss \(\Phi \)gemessen, der von einem Magnetpol ausgeht und durch eine Fläche fließt.
Die Polstärke \(\overrightarrow p \) gibt die Stärke und die Orientierung der beiden Pole eines Magneten an.
Weber
Weber → Magnetostatik; Coulomb → Elektrostatik;
Das Weber Wb ist die Einheit der magnetischen Polstärke bzw. vom magnetischen Fluss. Da es keine räumlich isolierten magnetischen Monopole gibt, wird die Polstärke durch den magnetischen Fluss \(\Phi \) gemessen, der von einem Magnetpol ausgeht und durch eine Fläche fließt.
1 Weber Wb ist der magnetische Fluss, der in einer Leiterschleife von 1 m², bei konstanter zeitlicher Änderung des Flusses innerhalb von 1 Sekunde eine Spannung von 1 Volt induziert.
Die Einheit der magnetischen Polstärke, bzw. vom magnetischen Fluss ergibt sich gemäß folgender Einheitengleichung
\(\left[ \Phi \right]{\rm{ = }}\left[ V \right] \cdot \left[ {\rm{t}} \right]{\rm{ = 1V}} \cdot {\rm{1s = 1Vs = 1Wb = 1T}} \cdot {{\rm{m}}^2}\)
Magentische Kraft zwischen zwei Magnetpolen
Magnetisches Kraftgesetz → Magnetostatik; Coulombsches Gesetz → Elektrostatik;
Das Magnetische Kraftgesetz stellt einen Zusammenhang zwischen der magnetischen Größe „Fluss“ bzw. magnetische Flussdichte B“ und der mechanischen Größe „Kraft“ her. Man kann daher analog zum Coulombschen Gesetz das Magnetische Kraftgesetz wie folgt anschreiben
\(F = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{\Phi _1} \cdot {\Phi _2}}}{{{r^2}}} = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{B_1} \cdot {A_1} \cdot {\Phi _2} \cdot {A_2}}}{{{r^2}}} = k \cdot \dfrac{{{p_1} \cdot {p_2}}}{{{r^2}}}\)
Beispiel: Überprüfen wir das Magnetische Kraftgesetz mittels einer Einheitengleichung:
\(\begin{array}{l} F = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{\Phi _1} \cdot {\Phi _2}}}{{{r^2}}} = \dfrac{1}{{4\pi {\mu _0}}} \cdot \dfrac{{{B_1} \cdot {A_1} \cdot {\Phi _2} \cdot {A_2}}}{{{r^2}}}\\ N = \dfrac{1}{{\frac{{Vs}}{{Am}}}} \cdot \dfrac{{W{b^2}}}{{{m^2}}} = \dfrac{{Am \cdot W{b^2}}}{{Vs \cdot {m^2}}} = \dfrac{{A \cdot W{b^2}}}{{Vs \cdot m}} = \\ \\ {\rm{mit Wb}} = Vs = \dfrac{{Nm}}{A} \to V = \dfrac{{Nm}}{{As}}\\ = \dfrac{{A \cdot \dfrac{{{N^2} \cdot {m^2}}}{{{A^2}}}}}{{\dfrac{{Nm}}{{As}} \cdot s \cdot m}} = \dfrac{{A \cdot {N^2} \cdot {m^2} \cdot A \cdot s}}{{{A^2} \cdot N \cdot s \cdot {m^2}}} = N\,\,\,\,{\rm{wzbw}}{\rm{.}} \end{array}\)
Das Magentische Kraftgesetz gibt ein Maß / eine Formel für jene Kraft an, die 2 magnetische Pole auf einander ausüben und zwar zufolge der magnetischen Polstärke. Der Raum zwischen den Polen ist von einem elektromagnetischen Feld erfüllt. Das magnetische Feld ist eine Folge der subatomaren Bewegung von Elektronen auf deren Umlauf um den Atomkern.
Das Quant / das Boson der fundamentalen elektromagnetischen Wechselwirkung ist das Photon, welches daher der Vermittler der anziehenden oder abstoßenden Kräfte zwischen den beiden Magnetpolen ist.
Das magnetische Feld
Magnetisches Feld → Magnetostatik; Elektrisches Feld → Elektrostatik;
Sind in einem Raum bewegte elektrische Ladungen vorhanden, so verursachen diese bewegten Ladungen die Ausbildung eines magnetischen Feldes \(\overrightarrow H\). In Dauermagneten fließen diese das Magnetfeld verursachenden Ströme in Form von bewegten Elektronen auf atomarer Ebene. Das Erdmagnetfeld wird durch die Bewegung von flüssiger leitfähiger Metallschmelze im Erdkern, in einem natürlich vorhandenem Initialfeld, induziert. Zufolge des magnetischen Feldes wirkt auf bewegte geladene Teilchen die sogenannte Lorentzkraft FL.
Magnetische Feldlinien
Magnetische Feldlinien → Magnetostatik; Elektrische Feldlinien → Elektrostatik;
Magnete und bewegte elektrische Ladungen, etwa in Form eines stromdurchflossenen Leiters, sind von einem magnetischen Feld \(\overrightarrow H \) umgeben. Stromfluss verändert nämlich den umgebenden Raum, indem er dort ein magnetisches Feld erzeugt.
Magnetische Feldlinien zeigen den Verlauf des Feldes, wobei magnetische Feldlinien immer geschlossen sind oder sie winden sich unendlich, ohne in sich zurückzulaufen, man spricht daher von einem sogenannten Wirbelfeld. Es gibt keine offenen - also nur geschlossene - magnetischen Feldlinien, weil ein Wirbelfeld keine Quellen und keine Senken hat. Magnetische Feldlinien verlaufen in Richtung vom Nord- zum Südpol.
Die Dichte der Feldlinien (also wie eng oder weit die Feldlinien auseinander liegen) ist ein Maß für die Feldstärke.
Magnetische Feldstärke
Magnetische Feldstärke → Magnetostatik; Elektrische Feldstärke → Elektrostatik;
Die magnetische Feldstärke \(\overrightarrow H\) oder auch magnetische Erregung genannt, ist eine vektorielle Größe, welche die Stärke und die Richtung eines magnetischen Feldes und somit die Fähigkeit des magnetischen Feldes, eine Kraft auf einen darin enthaltenen magnetischen Pol auszuüben, angibt. Ihre Ursache sind elektrische Ströme. Ihre Einheit ist Ampere pro Meter \(\left[ H \right] = \dfrac{A}{m}\). Die magnetische Feldstärke entspricht der magnetischen Spannung Um, bzw. der magnetischen Durchflutung Theta, beide in Ampere A, bezogen auf die Wegeinheit l.
\(\overrightarrow H = \dfrac{{\Delta {U_m}}}{{\Delta l}} = \dfrac{{\Delta \Theta }}{{\Delta l}}\)
Magnetische Flussdichte
Magnetische Flussdichte → Magnetostatik; Elektrische Flussdichte → Elektrostatik;
Die magnetische Flussdichte \({\overrightarrow B }\), auch magnetische Induktion genannt, ist ein vektorielles Maß für die örtliche Intensität des Magnetfeldes, zufolge einer magnetischen Feldstärke \( \overrightarrow H\) . Die beiden Größen sind im Vakuum über die magnetische Feldkonstante \({\mu _0}\) verknüpft. Die magnetische Feldkonstante \(\mu={\mu _r} \cdot {\mu _0}\) ist ein Maß für die Durchlässigkeit eines Materials für magnetische Felder.
\(\begin{array}{l} \overrightarrow B = {\mu _r} \cdot {\mu _0} \cdot \overrightarrow H \\ \left[ {\overrightarrow B } \right] = \dfrac{{{\rm{Vs}}}}{{{\rm{A}} \cdot {\rm{m}}}} \cdot \dfrac{{\rm{A}}}{{\rm{m}}}{\rm{ = }}\dfrac{{{\rm{Wb}}}}{{{{\rm{m}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{\rm{N}}}{{{\rm{A}} \cdot {\rm{m}}}}{\rm{ = T}} \end{array}\)
mit:
\({\mu _0} = 4\pi \cdot {10^{ - 7}}\dfrac{{Vs}}{{Am}}\)
Die magnetische Flussdichte \({\overrightarrow B }\) ist ein auf den Querschnitt bezogener Fluss \(\vec B = \dfrac{{d{\rm{\Phi }}}}{{dA}}\) und erlaubt im Gegensatz zum querschnittsabhängigen Fluss \(\Phi \) eine Exklusivaussage über die herrschende Feldstärke.
Magnetische Flussdichte B um einen stromdurchflossenen Leiter
Fließt durch einen unendlich langen geraden Leiter ein Strom der Stärke I, so ergibt sich der Betrag der magnetischen Flussdichte B im Abstand r vom Leiter wie folgt:
\(B = {\mu _0} \cdot \dfrac{1}{{2\pi r}} \cdot I\)
Die Feldlinien des Magnetfeldes verlaufen dabei in konzentrischen Kreisen senkrecht zum stromdurchflossenen Leiter.
Magnetische Flussdichte B im Inneren einer stromdurchflossenen Spule
\(\overrightarrow B = \dfrac{{n \cdot {\mu _0} \cdot I}}{{{l_{Spule}}}}\)
bzw. wenn die Spule einen Kern hat:
\(\overrightarrow B = \dfrac{{n \cdot {\mu _r} \cdot {\mu _0} \cdot I}}{{{l_{Spule}}}}\)
Tesla (T)
Das Tesla T ist die Einheit der magnetischen Flussdichte. Einem Tesla entspricht jene magnetische Flussdichte, die auf einen 1m langen Leiter, der von einem Strom von 1 A durchflossen wird, eine Kraft von 1 N ausübt. 1 T ist eine sehr große Einheit.
\(\left[ {1 \cdot T = 1 \cdot \dfrac{{V \cdot s}}{{{m^2}}} = 1 \cdot \dfrac{N}{{A \cdot m}} = 1 \cdot \dfrac{{Wb}}{{{m^2}}} = 1 \cdot \dfrac{{kg}}{{A \cdot {s^2}}}} \right]\)
- Das Erdmagnetfeld beträgt ca \(4 \cdot {10^{ - 5}}T\).
- In der Magnetresonanztomographie, einem bildgebenden Verfahren zur Darstellung der Gewebestruktur, erzeugt ein 34 Tonnen Magnet mit 270 Tonnen Eisen zur Abschirmung bis zu 7 Tesla.
Unterschied zwischen Induktion B und Induktivität L
Die magnetische Flussdichte B wird manchmal auch magnetische Induktion genannt. Da "Induktion" und "Induktivität" auf Grund der gemeinsamen ersten 7 Buchstaben sehr ähnlich klingen, sei hier auf den Unterschied hingewiesen.
- Magnetische Flussdichte B - sie wird auch magnetische Induktion genannt - ist ein Maß dafür, wie stark ein Magnetfeld ist. Ihre Einheit ist das Tesla.
- Induktivität L ist eine Eigenschaft einer Spule und hängt nur von deren geometrischer Bauform ab. Ihre Einheit ist das Henry.
Magnetischer Fluss Phi
Magnetische Fluss → Magnetostatik; Elektrische Fluss → Elektrostatik;
Allgemein bezeichnet man jedes Flächenintegral über eine Vektorgröße als Fluss. Der magnetische Fluss \(\Phi\) (sprich: “Phi“) mit der Einheit Weber, ist ein Maß dafür, wie viel Feld \(\overrightarrow B\) etwa aus dem N-Pol eines Magneten austritt. Er gibt die Gesamtzahl aller Feldlinien an, die von einer Spule erzeugt werden.
\(\begin{array}{l} \Phi = \int\limits_A {\overrightarrow B \,\,d\overrightarrow A } \\ \left[ \Phi \right] = Wb \end{array}\)
Der magnetische Fluss \(\Phi\) ist ein Skalar. Der magnetische Fluss ist nur für eine Fläche im Raum definiert, daher auch das Flächenintegral, nicht aber für jeden einzelnen Punkt im Raum. In der Praxis wird daher selten mit dem magnetischen Fluss, sondern mit der magnetischen Flussdichte B gearbeitet.
- Im inhomogenen Feld ergibt sich der magnetische Fluss \(\Phi\), wenn man die magnetische Flussdichte \(\overrightarrow B\) über den Querschnitt \(\overrightarrow A\) aufsummiert (aufintegriert).
- Im homogenen Feld ist der magnetische Fluss \(\Phi\) das „in-Produkt“ aus Felddichte \(\overrightarrow B\) und orientiertem Querschnitt \(\overrightarrow A\) gemäß: \(\Phi = \overrightarrow B \cdot \overrightarrow A \cdot \cos \left( {\angle \overrightarrow B ,\overrightarrow A } \right)\). Der magnetische Fluss hat sein Maximum wenn \(\overrightarrow B \parallel \overrightarrow A\)
Der magnetische Fluss \(\Phi\) ist - vergleichbar zur elektrischen Stromstärke I - die Wirkung einer magnetischen Spannung Um und fließt durch einen materialabhängigen magnetischen Widerstand Rm.
Nachfolgende Gleichung liefert den Zusammenhang zwischen magnetischem Fluss Phi und magnetischer Durchflutung Theta:
\(\Phi = \dfrac{{{U_m}}}{{{R_m}}} = \dfrac{\Theta }{{{R_m}}}\)
Magnetische Durchflutung Theta, zugleich magnetische Spannung Um
Die magnetische Durchflutung \(\Theta\) dient zur Berechnung einer, durch einen elektrischen Storm erzeugten, magnetischen Feldstärke.
\(\Theta = \sum\limits_k {{I_k}} = \int\limits_A {\overrightarrow S \,\,d\overrightarrow A } = {U_m}\)
Die magnetische Durchflutung einer Spule ergibt sich aus Strom mal Windungszahl.
\(\Theta = I \cdot n\)
Die Einheit der magnetischen Durchflutung ist das Ampere bzw. die Amperewindungen.
Eine Spule mit 600 Windungen übt bei einem Strom von 2A eine gleich große Kraft auf ein Eisenstück aus, wie eine Spule mit 1200 Windungen und einem Strom von 1A. Die Windungszahl n hat als Einheit 1.
Die magnetische Durchflutung \(\Theta \) bzw die magnetische Spannung, ist die Ursache für das Vorhandensein einer magnetischen Feldstärke H.
Der nachfolgende Zusammenhang wird Durchflutungssatz genannt und in der Mikro-Lerneinheit „Elektrodynamik“ näher besprochen
\(\Theta = {U_m} = \mathop \oint \limits_s \vec H{\mkern 1mu} {\mkern 1mu} d\vec s = \mathop \smallint \limits_A \vec S{\mkern 1mu} {\mkern 1mu} d\vec A = \mathop \sum \limits_k {I_k}\)
Zusammenhang elektrische Feldkonstante, magnetische Feldkonstante und Lichtgeschwindigkeit
Die Lichtgeschwindigkeit verknüpft die elektrischer Feldkonstante und magnetischer Feldkonstante wie folgt:
\({c_0} = \dfrac{1}{{\sqrt {{\varepsilon _0} \cdot {\mu _0}} }}\)
Magnetische Feldkonstante Mü
Magnetische Feldkonstante → Magnetostatik; Elektrische Feldkonstante → Elektrostatik;
Unterschiedliche Materialien haben eine unterschiedliche Durchlässigkeit für magnetische Felder. Das Maß dafür ist die magnetische Feldkonstante bzw. Permeabilität \({\mu}\). Die magnetische Durchlässigkeit eines Stoffs \({\mu}\) (sprich: „Mü“), ist das Produkt aus der magnetischen Feldkonstante die im Vakuum gilt \({\mu _0}\) und einem materialspezifischen dimensionslosen Faktor \({\mu _r}\)
Für Luft ist \({\mu _r} \approx 1\). Luft und Vakuum leiten daher sehr schlecht. Ferromagnetische Stoffe hingegen haben eine hohe magnetische Durchlässigkeit \({\mu _{r,\,Fe}} \approx 200\). D.h. die magnetischen Kraftlinien schließen sich bevorzugt über Eisenwege und nur kleine Streuanteile gehen über Luft. Die magnetische Leitfähigkeit von CU: \({\mu _{r,\,Cu}} \approx 1\)
\(\eqalign{ & \mu = {\mu _r} \cdot {\mu _0} \cr & \left[ \mu \right] = \dfrac{{Vs}}{{Am}} \cr & \left[ {{\mu _r}} \right] = 1 \cr & {\mu _0} = \dfrac{1}{{{\varepsilon _0} \cdot {c^2}}} = 4 \cdot \pi \cdot {10^{ - 7}}\dfrac{{Vs}}{{Am}} \cr} \)
Materialien unterscheiden sich erheblich bezüglich ihrer relativen Permeabilität. Diamagnetische Stoffe besitzen eine relative Permeabilität zwischen 0 und 1. Ein Supraleiter 1. Art verdrängt ein von außen vorhandenes Magnetfeld vollständig aus seinem Inneren und hat daher \({\mu _{r,Supraleiter}} = 0\). Für Wasser und Luft gilt: \({\mu _{r,H2O}} = 0,999991;\,\,\,\,\,{\mu _{r,Luft}} = 1,0000004\). Für Eisen gilt der Bereich \({\mu _{r,Eisen}} \approx 300...10000\). Für amorphe oder nanokristalline Metalle liegt die relative Permeabilität bei Werten bis einige Hundertausend.
Um eine bestimmte magnetische Induktion L etwa in Eisen hervorzurufen, bedarf es zufolge \(\overrightarrow B = \mu \cdot \overrightarrow H\) einer weit geringeren magnetischen Feldstärke \( \overrightarrow H\) , als etwa für die gleiche magnetische Induktion L in Luft erforderlich wäre. Wenn allerdings im Eisen alle Elementarmagnete ausgerichtet sind, d.h. im Bereich sehr hoher Sättigung, ist die Zunahme der magnetischen Flussdichte \(\overrightarrow B\) bei weiterer Steigerung der äußeren magnetischen Feldstärke \(\overrightarrow H\) schließlich nicht mehr größer als in Luft.
Rechnenbeispiel zum Zusammenhang: magn. Durchflutung, magn. Feldstärke und magn. Flussdichte
Eine Spule mit n=5000 Windungen wird von einem Strom I=10mA durchflossen.
1. Teilaufgabe
Wie groß ist die magnetische Durchflutung der Spule?
\(\Theta = \sum\limits_k {{I_k}} \)
\(\Theta = I \cdot n = \left( {10 \cdot {{10}^{ - 3}}} \right) \cdot \left( {5 \cdot {{10}^3}} \right) = 50A\)
Die Länge einer mittleren Feldlinie beträgt 20cm.
2. Teilaufgabe
Wie groß ist die magnetische Feldstärke?
\(H = \dfrac{\Theta }{{{l_{Mittel}}}} = \dfrac{{50A}}{{0,2m}} = 250\frac{A}{m}\)
Bei der Spule handle es sich um eine Luftspule mit \({\mu _r} = 1\)
3. Teilaufgabe
Wie groß ist die magnetische Flussdichte?
\(B = {\mu _0} \cdot {\mu _r} \cdot H = 4 \cdot \pi \cdot {10^{ - 7}} \cdot 1 \cdot 250 \approx 0,314mT\)
In die Luftspule wird ein Eisenkern mit \({\mu _r} = 6000\) eingebracht.
4. Teilaufgabe
Wie groß ist die magnetische Flussdichte?
\(B = {\mu _0} \cdot {\mu _r} \cdot H = 4 \cdot \pi \cdot {10^{ - 7}} \cdot 6000 \cdot 250 \approx 1,885T\)
In dieser Mikro-Lerneinheit lernst du die wesentlichen physikalischen Größen sowie die Grundgleichungen der Elektrodynamik kennen, ohne dass wir auf deren Herleitung (Uni-Niveau) eingehen.
Diese Lerneinheit ist mathematisch anspruchsvoll, da zeitlich veränderliche Felder mittels Werkzeuge wie Rotor und Divergenz aus der Vektor-Differentialgeometrie behandelt werden. Du solltest daher mit den Mikro-Lerneinheiten zur Vektoranalysis, der Elektrostatik und der Magnetostatik vertraut sein, ehe du die Miko-Lerneinheit Elektrodynamik beginnst.
Zunächst gehen wir auf weitere Grundlagen der Elektrodynamik wie die Lenzschen Regel, die Urspannung, das Faradaysche Induktionsgesetz, das 1. Amperesche Gesetz bzw. die Lorenzkraft auf bewegte Ladungen, sowie auf das 2. Amperesche Gesetz – das Durchflutungsgesetz – ein. Wir stellen den elektrischen Hüllenfluss und den magnetischen Hüllenfluss vor, bei denen der gaußsche Integralsatz zur Anwendung kommt.
Wir lernen die Polarisierung und die Magnetisierung kennen und beschäftigen uns mittels der 4 Maxwellgleichungen mit elektrischen und magnetischen Feldern, sowohl im stationären als auch im sich zeitlich rasch ändernden Zustand. Mit Hilfe der Integralsätze von Stokes und Gauß können die 4 Maxwellgleichungen aus der Integralform in die Differentialform gebracht werden.
Zuletzt gehen wir auf die Wellengleichung der elektromagnetischen Welle ein und geben einen Überblick über die über die Elektrodynamik hinausgehende Bedeutung der Maxwell Gleichungen.
Elektrodynamik
Erforderliches Vorwissen zum Verständnis der 4 maxwellschen Gleichungen
Nachfolgend fassen wir einige Regeln zu elektromagnetischen Feldern zusammen, die Maxwell zu den nach ihm benannten Gleichungen veranlasst haben
Lentzsche Regel
Die induzierte Feldstärke ist immer so gerichtet, dass das Magnetfeld eines in einer gedachten Leiterschleife fließenden Stroms, dem erzeugenden Magnetfeld im Eisenkern entgegen gerichtet ist. Die am Ort der Leiterschleife vorhandene elektrische Wirbelfeldstärke \(\overrightarrow E\) ist eingeprägt - sie wird nicht von der Leiterschleife kurzgeschlossen. Die lentzsche Regel liefert die Ursache für das negative Vorzeichen in der 3. maxwellschen Gleichung.
\(\mathop {{U_e}}\limits^o = \oint\limits_s {\overrightarrow E \,\,d\overrightarrow s } = - \dfrac{{d\Phi }}{{dt}} = - \dfrac{d}{{dt}}\int\limits_A {\overrightarrow B \,\,d\overrightarrow A = - \int\limits_A {\dfrac{{d\overrightarrow B }}{{dt}}\,\,d\overrightarrow A } } \)
Urspannung oder Quellenspannung
Bei der Urspannung handelt es sich um die in die Wicklungen von elektrischen Maschinen induzierte Spannung, die früher auch EMK „Elektromotorische Kraft“ genannt wurde.
- Die Urspannung ist die in den Wicklungen der Maschine induzierte Spannung, die an den Klemmen einer elektrischen Maschine anliegt, ohne Einfluss eines Stromflusses über deren Innenwiderstände.
- Die Klemmenspannung ist die Spannung, die an den Klemmen einer elektrischen Maschine anliegt, wenn sie belastet ist. Sie ist also die Spannung, die ein Generator an die Verbraucher im Netz liefert oder die externe Netzspannung, die ein Motor benötigt, damit der die Nennleistung erbringt.
Der veraltete Begriff EMK erklärt sich damit, dass die EMK mit dem Kehrwert der Ladung proportional zur coulombschen Kraft ist. Die EMK entspricht der Fähigkeit eines Systems, eine Spannung – die „Urspannung“ mit der Einheit Volt (V) - zu erzeugen.
Die Urspannung entsteht, wenn es zu einer Änderung des magnetischen Flusses durch eine Leiterschleife kommt. Dies kann auf 2 Arten geschehen:
- Bewegungsinduktion: Die magnetische Flussdichte B ist konstant, und die Spule bewegt sich darin
- Ruheinduktion: Die Spule ruht, und die magnetische Flussdichte B ändert sich zeitlich
Bildet man aus der Gleichung für die Lorentzkraft auf bewegte Ladungen
\(\overrightarrow {{F_L}} = Q \cdot \left( {\overrightarrow v \times \overrightarrow B } \right)\)
den Quotient aus Lorentzkraft und Ladung, so erhält man die elektrische Feldstärke Eb, wobei der Index „b“ für „bewegte Ladung“ steht.
\(\overrightarrow {{E_b}} = \dfrac{{\overrightarrow {{F_L}} }}{Q} = \overrightarrow v \times \overrightarrow B \)
Bewegungsinduktion eib - Spule bewegt sich
Durch die Bewegung der Spule in einem Magnetfeld B wird, zufolge der auf die beweglichen Ladungsträger des Leiters ausgeübte Lorentzkraft, eine Urspannung induziert. Das Linienintegral zwischen 2 Klemmen einer Leiterschleife heißt „induzierte Urspannung zufolge der Bewegung“. Sie entsteht, wenn das Magnetfeld B konstant bleibt, und sich darin eine Spule bewegt
\({e_{ib,12}} = \int\limits_1^2 {{E_b}\,ds} = \int\limits_1^2 {\left( {\overrightarrow v \times \overrightarrow B } \right)} \,\,ds\)
Ruheinduktion eir - Spule ruht
Durch die zeitliche Änderung des magnetischen Feldes B entsteht im ganzen umgebenden Raum ein elektrisches Wirbelfeld, wodurch eine Urspannung in die ruhende Spule induziert wird. Das Flächenintegral über alle durch die Änderung der magnetischen Flussdichte B gemäß der 2. maxwellschen Gleichung verursachten Wirbel des elektrischen Feldes E ergibt:
\({e_{ir}} = \int\limits_A {rot\overrightarrow E \cdot d\overrightarrow A } = - \int\limits_A {\dfrac{{\partial \overrightarrow B }}{{\partial t}}} \,d\overrightarrow A \)
Faradaysches Induktionsgesetz
Das faradaysche Induktionsgesetz besagt, dass jede Änderung des magnetischen Flusses \(\Phi\) durch eine verkettete Leiterschleife, egal ob diese durch die Bewegung einer Spule im Magnetfeld (Bewegungsinduktion) oder zufolge einer zeitlichen Änderung des Magnetfeldes (Ruheinduktion) verursacht ist, eine elektromotorische Kraft (EMK) bewirkt, und somit eine Urspannung induziert.
Das Faradaysche Induktionsgesetz beschreibt, wie ein sich änderndes magnetisches Feld einen elektrischen Strom in einem Leiter erzeugt und gehört daher in den Bereich der Elektrodynamik. Das „Minuszeichen“ ergibt sich zufolge der lentzschen Regel.
\({u_i} = {u_{ib}} + {u_{ir}} = - \int\limits_A {\dfrac{{d\overrightarrow B }}{{dt}}} \,d\overrightarrow A + \int\limits_1^2 {\left( {\overrightarrow v \times \overrightarrow B } \right)} \,\,ds = - \dfrac{{d\Phi }}{{dt}} = \oint\limits_A {\overrightarrow E } \,\,d\overrightarrow s \)
Es kommt dabei nicht darauf an, ob sich der mit der Spule verkettete Fluss zufolge der Bewegung der Spule oder zufolge der Änderung des magnetischen Flusses ändert.
Die Induktionswirkung kommt zustande, weil ein sich zeitlich ändernder magnetische Fluss \(\dfrac{{d\Phi }}{{dt}}\) von einem elektrischen Wirbelfeld \(\overrightarrow E\) mit geschlossenen Feldlinien umgeben ist. Die induzierte elektrische Spannung Ui ist der zeitlichen Änderung des magnetischen Flusses \(\Phi\) proportional und somit ein Maß für die Stärke der Wirbel des magnetischen Feldes, also von \(\Phi\) oder \(\overrightarrow B\) Feldlinien im Eisenkreis.
1. Ampere’sches Gesetz bzw. Lorentzkraft auf bewegte Ladungen
Fließt ein Gleichstrom durch einen von 2 parallelen Leitern, so umgibt ein Magnetfeld B diesen Leiter. Dieses Magnetfeld übt auf den zweiten, von keinem Strom durchflossenen Leiter keine Kraft aus, weil dessen Ladungen ruhen.
Fließt aber zusätzlich auch durch den 2. Leiter ein Gleichstrom, und bewegen sich daher dessen Ladungen, dann geht vom Magnetfeld des 1. Leiters eine Lorentzkraft auf diese bewegten Ladungen aus.
Bei gleichorientiertem Stromfluss ziehen sich die beiden Leiter an, bei entgegengesetztem Stromfluss stoßen sie sich gegenseitig mit der Kraft F ab.
Beispiel:
Fließen die Gleichströme I1=I2 der Stärke 1A durch 2 gerade, parallele Drähte, die einen Abstand von 1m zueinander haben, so bewirkt das Magnetfeld B1 zufolge des Stromflusses I1 eine Lorentzkraft F2 an der Stelle vom 2. Leiter von 2·10-7 N/m.
\({F_2} = l \cdot {I_2} \cdot {B_1} = {\mu _0} \cdot \dfrac{{{I_1} \cdot {I_2}}}{{2\pi r}} \cdot l\) zufolge des Magnetfeldes \({B_1} = \dfrac{{{\mu _0} \cdot {I_1}}}{{2\pi \cdot r}}\)
Die Lorentzkraft stellt einen Zusammenhang zwischen einem magnetischen Feld und einer Kraft auf einen stromdurchflossenen Leiter bzw. dessen bewegte Ladungen dar. Die Lorentzkraft wirkt auf bewegte Ladungen im Magnetfeld und ist daher ein Phänomen der Elektrodynamik
Die Lorentzkraft wirkt senkrecht zur Bewegungsrichtung des geladenen Teilchens und senkrecht zur Richtung vom Magnetfeld. Die Lorentzkraft führt dazu, dass sich Elektronen in einem Magnetfeld auf gekrümmten Bahnen bewegen. In einem Elektromotor ist es die Lorentzkraft, die dafür sorgt, dass sich der Anker unter der Einwirkung des, von den Wicklungen im Stator ausgehenden, Magnetfelds dreht.
Lorentzkraft auf punktförmiges geladenes Teilchen
Befindet sich ein geladenes Teilchen in einem Magnetfeld, so wirkt die Lorentzkraft auf das Teilchen.
\(\overrightarrow {{F_L}} = Q \cdot \left( {\overrightarrow v \times \overrightarrow B } \right)\)
Mit FL als Lorentzkraft in N, Q als Ladung des Teilchens in C, v der Geschwindigkeit des Teilchens in m/s und B der magnetischen Flussdichte in T.
Lorentzkraft auf inkrementell kurzes Leiterstück ds
Befindet sich ein stromdurchflossener Leiterdraht in einem Magnetfeld, so ist die Höhe der Lorentzkraft FL proportional zur Stromstärke i die durch den Leiter fließt, zur Länge s des stromdurchflossenen Leiters und zur magnetischen Flussdichte B, welche die Stärke des Magnetfeldes an einem bestimmten Punkt und in eine bestimmte Richtung beschreibt.
\(d\overrightarrow F = i \cdot \left( {d\overrightarrow s \times \overrightarrow B } \right)\)
Lorentzkraft auf Leiter der Länge l
Für die gesamte Länge des Leiters aufintegriert ergibt sich wie folgt, wobei falls B senkrecht auf l steht, wie folgt vereinfacht werden kann:
\(\overrightarrow {{F_L}} = i \cdot \int\limits_0^l {\left( {d\overrightarrow s \times \overrightarrow B } \right)} = i \cdot \left( {\overrightarrow l \times \overrightarrow B } \right)\)
Durchflutungsgesetz, auch amperescher Durchflutungssatz bzw. 2. amperesches Gesetz
Der Durchflutungssatz besagt, dass in einem magnetischen Feld das Linienintegral über die magnetische Feldstärke H entlang einer in sich geschlossenen Feldlinie \(\oint\limits_s {\overrightarrow H } \,\,d\overrightarrow s \)
- stets gleich dem gesamten elektrischen Strom ist, der durch die von dieser Feldlinie gebildeten Fläche hindurchtritt \( \sum\limits_k {{I_k}} \)
- gleich – und nicht lediglich proportional - ist, der magnetischen Durchflutung Theta \(\Theta = {U_m}\)
Der Durchflutungssatz besagt, dass geschlossene magnetische Feldlinien von einem Strom durchflossen bzw. „durchflutet“ werden, bzw. umgekehrt formuliert, dass ein elektrischer Strom von geschlossenen magnetischen Feldlinien umgeben ist.
So wie im elektrischen Feld die elektrische Spannung durch Feldstärke mal Weg definiert ist, führt man auch im magnetischen Feld eine magnetische Spannung Um ein. Sie ist ein Skalar mit der Einheit Ampere (A). Die Einheit der magnetischen Durchflutung ist das Ampere (A)
\(\Theta = {U_m} = \oint\limits_s {\overrightarrow H } \,\,d\overrightarrow s = \int\limits_A {\overrightarrow S \,\,d\overrightarrow A } = \sum\limits_k {{I_k}} \)
Multipliziert man obige Gleichung mit der magnetischen Feldkonstanten im Vakuum, erhält man
\({\mu _0} \cdot \Theta = \oint\limits_s {\overrightarrow B } \,\,d\overrightarrow s = {\mu _0} \cdot \int\limits_A {\overrightarrow S \,\,d\overrightarrow A } \)
Es ist also das Linienintegral der magnetischen Flussdichte B, entlang eines geschlossenen Weges s (etwa der Windung einer Spule), proportional (mit der magnetischen Feldkonstanten bzw. der magnetischen Permeabilität) der durch die Fläche, deren Randkurve der gewählte geschlossene Weg ist, hindurchfließende, somit „durchflutende“ Gesamtstromstärke.
Anmerkung: S=J .. elektrische Stromdichte S (oft auch mit J bezeichnet - wir verwenden J jedoch für die magnetische Polarisation), ist der Quotient aus Stromstärke I und Leiterquerschnittsfläche A
Das amperesche Durchflutungsgesetz mit dem Maxwell-Ergänzungsterm – also die 4. Maxwellgleichung - besagt, dass die magnetische Feldstärke proportional zur elektrischen Stromdichte und der Änderung des elektrischen Feldes ist.
\(rot\vec H = \overrightarrow {{S_L}} + \dfrac{{d\vec D}}{{dt}}\)
Magnetische Durchflutung einer Spule mit n Windungen
\(\Theta = n \cdot I\)
Elektrischer Hüllenfluss
Der Satz vom elektrischen Hüllenfluss besagt, dass der durch eine Fläche austretende Fluss, gleich der im Volumen eingeschlossenen Ladung ist.
\(\mathop \psi \limits^o = \oint\limits_A {\overrightarrow D } \,\,d\overrightarrow A = \int\limits_V {\operatorname{div} \overrightarrow D \,\,dV} = \int \varphi \,\,dV = \sum\limits_{k = 1}^n {{Q_k}} \)
In obiger Gleichung kommt der gaußsche Integralsatz zur Anwendung.
Magnetischer Hüllenfluss
Der Satz vom magnetischen Hüllenfluss besagt, dass der durch eine Fläche austretende magnetische Fluss, auf Grund der Quellenfreiheit magnetischer Felder stets gleich Null sein muss.
\(\mathop \Phi \limits^o = \oint\limits_A {\overrightarrow B \,\,d\overrightarrow A } = \int\limits_V {\operatorname{div} \overrightarrow B \,\,dV} = 0\)
In obiger Gleichung kommt der gaußsche Integralsatz zur Anwendung.
Elektrodynamik
Die Elektrodynamik ist eine Feldtheorie für das elektrische und das magnetische Feld, wobei zu jedem Zeitpunkt t und an jedem Raumpunkt \(\overrightarrow x\) je ein Vektor \(\overrightarrow D \, - \,\overrightarrow E \, - \,\overrightarrow B \, - \,\overrightarrow H \) definiert ist. Die 4 maxwellschen Gleichungen bilden die Basis der Theorie des elektromagnetischen Feldes.
Die Elektrodynamik beschreibt einen von den 4 vektoriellen Feldgrößen \(\overrightarrow D \, - \,\overrightarrow E \, - \,\overrightarrow B \, - \,\overrightarrow H \) erfüllten Raum.
elektrisches Feld, beschrieben durch die elektrische Feldstärke und die elektrische Flussdichte
\(\vec E\left( {\vec x,t} \right){\mkern 1mu} {\text{ in }}\dfrac{{\text{V}}}{{\text{m}}}{\text{ bzw}}{\text{. }}\vec D\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{C}}}{{{{\text{m}}^{\text{2}}}}}\)
magnetisches Feld, beschrieben durch die magnetische Feldstärke und die magnetische Flussdichte
\(\vec H\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{A}}}{{\text{m}}}{\text{ bzw}}{\text{. }}\vec B\left( {\vec x,t} \right){\text{ in T}}\)
Verknüpfungsbeziehungen zwischen Flussdichten und Feldstärken
im stationären Feld:
\(\eqalign{ & \overrightarrow D = {\varepsilon _0} \cdot \overrightarrow E + \overrightarrow P \cr & \overrightarrow B = {\mu _0} \cdot \overrightarrow H + {\mu _0} \cdot \overrightarrow M = {\mu _0} \cdot \overrightarrow H + \overrightarrow J \cr} \)
im sich zeitlich rasch verändernden Feld:
\(\eqalign{ & \overrightarrow D = \varepsilon \cdot \overrightarrow E \cr & \overrightarrow B = \mu \cdot \overrightarrow H \cr} \)
Flussdichten: Mit \(\overrightarrow D {\text{ und }}\overrightarrow B \) stehen auf der linken Seite der Gleichung Flussdichten. Bei gegebener Flussdichte ist die Feldstärke umso größer, je kleiner die entsprechende Leitfähigkeit ist.
Feldstärken: Mit \(\overrightarrow E {\text{ und }}\overrightarrow H \) stehen auf der rechten Seite der Gleichungen Feldstärken. Bei gegebener Feldstärke ist die Flussdichte umso größer, je höher die entsprechende Leitfähigkeit ist.
Während \(\overrightarrow E {\text{ und }}\overrightarrow B \) ein Maß für die Stärke des Feldes (Intensitätsgröße) sind, ist die dielektrische Verschiebung \(\overrightarrow D \) bzw. die magnetische Erregung \(\overrightarrow H \) ein Maß für das Ausmaß der Wirkung des Feldes (Quantitätsgröße) auf ein konkretes Medium.
3 Materialgleichungen
Die 4 Feldgrößen \(\overrightarrow D \, - \,\overrightarrow E \, - \,\overrightarrow B \, - \,\overrightarrow H \) sind durch 3 Materialgleichungen mittels elektrischer bzw. magnetischer Feldkonstante und mittels der elektrischen Leitfähigkeit mit einander verknüpft:
\(\overrightarrow S = \kappa \cdot \overrightarrow E\) …\(\kappa\) = Konduktivität = elektrische Leitfähigkeit ("Kappa") \(\left[ \kappa \right] = \dfrac{A}{{Vm}}\)
\(\overrightarrow B = \mu \cdot \overrightarrow H\) … \(\mu\) = Permeabilität = magnetische Feldkonstante ("Mü") \(\left[ \mu \right] = \dfrac{{Vs}}{{Am}}\)
\(\overrightarrow D = \varepsilon \cdot \overrightarrow E\) … \(\varepsilon\) = Permittivität = elektrische Feldkonstante ("Epsilon") \(\left[ \varepsilon \right] = \dfrac{C}{{Vm}}\)
Ohmsches Gesetz des stationären Strömungsfeldes
\(\overrightarrow S = \kappa \cdot \overrightarrow E \)
Anmerkung: Die elektrische Stromdichte S wird auch oft mit J bezeichnet. Wir verwenden J aber für die magnetische Polarisation.
Die elektrische Stromdichte S ist der Quotient aus Stromstärke I und Leiterquerschnittsfläche A
\(\left[ S \right] = \dfrac{{\left[ {\text{I}} \right]}}{{\left[ {\text{A}} \right]}}{\text{ = }}\dfrac{{\text{A}}}{{{{\text{m}}^{\text{2}}}}}\)
Die elektrische Leitfähigkeit ("Kappa") \(\left[ \kappa \right] = \dfrac{{\text{A}}}{{{\text{Vm}}}}\) repräsentiert die "Reibung" der bewegten Ladungsträger am Ionengitter des Leitermaterials.
Polarisation und Magnetisierung
Elektrische Polarisation P
Unter elektrischer Polarisation versteht man eine Ladungsverschiebung in einem nichtleitenden Material, welche durch ein äußeres elektrisches Feld verursacht wird.
Anmerkung: Influenz hingegen bedeutet Ladungsverschiebung in einem leitenden Material durch ein äußeres elektrisches Feld.
\(\vec P\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{C}}}{{{{\text{m}}^{\text{2}}}}} = \dfrac{{{\text{A}} \cdot {\text{s}}}}{{{{\text{m}}^{\text{2}}}}}\)
\(\eqalign{ & \overrightarrow P = {\chi _{el}} \cdot {\varepsilon _0} \cdot \overrightarrow E \cr & \overrightarrow D = {\varepsilon _0} \cdot \overrightarrow E + \overrightarrow P \cr} \)
Mit \({\chi _{el}}\) (sprich „Chi“) als elektrische Suszeptibilität, einer dimensionslosen Materialkonstante, die angibt, wie stark sich ein Material unter dem Einfluss eines äußeren elektrischen Feldes polarisiert.
Magnetische Polarisation J
Unter magnetischer Polarisation versteht man die Ausrichtung von magnetischen Dipolen bzw. magnetischen Momenten in einem Material, welche durch ein äußeres magnetisches Feld verursacht wird. Magnetische Momente können parallel oder antiparallel zum äußeren Magnetfeld ausgerichtet sein. Ohne magnetische Polarisation gäbe es keine Magnetisierung.
\(\vec J\left( {\vec x,t} \right){\text{ in T bzw}}{\text{. }}\dfrac{{{\text{V}} \cdot {\text{s}}}}{{{{\text{m}}^{\text{2}}}}}{\text{ bzw}}{\text{. }}\dfrac{{{\text{Wb}}}}{{{{\text{m}}^{\text{2}}}}}\)
\(\eqalign{ & \overrightarrow B = {\mu _0}\overrightarrow H + {\mu _0}\overrightarrow M = {\mu _0}\overrightarrow H + \overrightarrow J \cr & \overrightarrow J = {\mu _0}\overrightarrow M \cr} \)
Magnetisierung M
Die Magnetisierung beschreibt die Entstehung eines makroskopischen Magnetfeldes zufolge des Umlaufs und der Rotation (Spin) von Elektronen auf ihren Elektronenbahnen. Sie ist ein Maß für die Stärke des magnetischen Feldes, welches durch magnetische Momente erzeugt wird.
\(\vec M\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{A}}}{{\text{m}}}\)
\(\overrightarrow M = {\chi _{mag}} \cdot \overrightarrow H \)
Mit \({\chi _{mag}}\) (sprich „Chi“) als magnetische Suszeptibilität, die angibt, wie das Verhältnis von Magnetisierung zur magnetischen Feldstärke ist. Ihre Einheit ist m³/kg. Die magnetische Suszeptibilität kann je nach Material positiv (magnetische Momente verstärken das äußere Magnetfeld), negativ oder null sein.
Stokesscher Satz und Gaußscher Satz
Mit Hilfe der Integralsätze von Stokes und Gauß können die 4 Maxwellgleichungen aus der Integralform in die Differentialform gebracht werden.
Satz von Stokes - Stokesscher Integralsatz
Der stokessche Integralsatz erleichtert die Integration, indem er ein Flächenintegral auf ein Linienintegral zurückführt.
Der Satz von Stokes besagt, dass das Integral über den Rotor eines Vektorfeldes über eine geschlossene Fläche A, gleich dem Linienintegral des Vektorfeldes über die Randkurve K der Fläche ist.
\(\begin{array}{*{20}{l}} {\int\limits_A {\left( {\vec \nabla \times \vec E} \right)} \cdot d\vec A = \oint\limits_{\partial A} {\vec E \cdot d\vec s} }\\ {\int\limits_A {\left( {\vec \nabla \times \vec H} \right)} \cdot d\vec A = \oint\limits_{\partial A} {\vec H \cdot d\vec s} } \end{array}\)
Satz von Gauß - Gaußscher Integralsatz
Der gaußsche Integralsatz erleichtert die Integration, da er ein Volumenintegral auf ein Flächenintegral zurückführt.
Der Satz von Gauß besagt, dass das Integral über die Divergenz eines Vektorfeldes innerhalb eines Volumen V, gleich dem Oberflächenintegral des Vektorfeldes über die Oberfläche A des betrachteten Volumens ist.
Allgemein bezeichnet man ein Flächenintegral über eine Vektorgröße als Fluss. Daher kann man auch formulieren:
Der Satz von Gauß stellt einen Zusammenhang zwischen der Divergenz eines Vektorfeldes in einem beliebigen Volumen V und dem Fluss des Feldes durch die Oberfläche A des betrachteten Volumens dar.
\(\begin{array}{*{20}{l}} {\int\limits_V {\left( {\vec \nabla \circ \vec B} \right)} \cdot dV = \oint\limits_A {\vec B} \cdot d\vec A}\\ {\int\limits_V {\left( {\vec \nabla \circ \vec D} \right)} \cdot dV = \oint\limits_A {\vec D} \cdot d\vec A} \end{array}\)
Für die Ladung q als Volumenintegral der Ladungsdichte \(\rho \) gilt:
\(q = \int\limits_V {\rho \cdot dV} \)
Die 4 Maxwell Gleichungen
Die 4 Maxwell Gleichungen bilden zusammen mit der Lorenzkraft das Fundament der Elektrodynamik.
Es handelt sich dabei um ein System auf partiellen Differentialgleichungen unter Verwendung der Operatoren div = Divergenz bzw rot = Rotation bzw. Nabla,
- für das elektrische Feld \(\vec E\left( {\vec x,t} \right){\mkern 1mu} {\text{ in }}\dfrac{{\text{V}}}{{\text{m}}}{\text{ bzw}}{\text{. }}\vec D\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{C}}}{{{{\text{m}}^{\text{2}}}}}\)
- für das magnetische Feld \(\vec H\left( {\vec x,t} \right){\text{ in }}\dfrac{{\text{A}}}{{\text{m}}}{\text{ bzw}}{\text{. }}\vec B\left( {\vec x,t} \right){\text{ in T}}\)
- für die Ladungsdichte \(\overrightarrow \rho \left( {\overrightarrow x ,t} \right){\text{ in }}\dfrac{{\text{C}}}{{{{\text{m}}^{\text{3}}}}}\)
- für den Stromdichtevektor \(\overrightarrow {{S_L}} \left( {\overrightarrow x ,t} \right){\text{ in }}\dfrac{{\text{A}}}{{{{\text{m}}^2}}}\)
Es treten dabei die
- elektrische Feldkonstante \({\varepsilon _0} = 8,854187817662 \cdot {10^{ - 12}}\dfrac{{{{\text{C}}^{\text{2}}}}}{{{\text{N}}{{\text{m}}^{\text{2}}}}}\)
- magnetische Feldkonstante \({\mu _0} = 4 \cdot \pi \cdot {10^{ - 7}}\dfrac{{N{s^2}}}{{{C^2}}}\)
auf, die folgenden Zusammenhang zur Lichtgeschwindigkeit c haben:
\({c_0} = \dfrac{1}{{\sqrt {{\varepsilon _0} \cdot {\mu _0}} }} \simeq 2,992 \cdot {10^8}\dfrac{{{\text{km}}}}{{\text{s}}}\)
Man unterscheidet folgende 4 Formen der Maxwellgleichungen:
nach der Art des Feldes:
- stationäres Feld: Die stationären Maxwellgleichungen gelten für zeitunabhängige Felder. Es kann das E und das B-Feld unabhängig voneinander betrachtet werden
- zeitlich rasch veränderliches Feld: Die dynamischen Maxwellgleichungen gelten auch für sich zeitlich rasch veränderliche Felder und sind eine Vervollständigung der statischen Maxwellgleichungen. Diese Formulierung der Maxwellgleichungen stellt ein System gekoppelter Differentialgleichungen dar.
nach der Schreibweise:
- Differentialform: Die Differentialform der Maxwellgleichungen geht von Wirbel- und Quellendichte, also von D, B aus.
- Integralform: Die Integralform der Maxwellgleichungen geht von Wirbel- und Quellenstärke also E, H aus.
1. Maxwellgleichung
Das Gaußsche Gesetz für elektr. Felder beschreibt den Zusammenhang zwischen elektr. Ladung im Raum und der Stärke des elektrischen Feldes. Die erste Maxwellgleichung besagt, dass Ladungen Q die Quellen des elektrischen Feldes sind.
1. Maxwellgleichung in Differentialform im statischen Feld
\(\nabla \cdot \overrightarrow D = div\overrightarrow D = \varphi _{wahr}^{el}\)
1. Maxwellgleichung in Differentialform im zeitlich veränderlichen Feld
\(\nabla \cdot \overrightarrow D = div\overrightarrow D = \varphi _{wahr}^{el}\)
1. Maxwellgleichung in Integralform
\(\oint\limits_A {\overrightarrow D } \,\,d\overrightarrow A = Q\)
2. Maxwellgleichung
Das Gaußsche Gesetz für magnetische Felder besagt, dass es keine magnetischen Monopole gibt. Die zweite Maxwellgleichung besagt, dass magnetische Felder immer quellenfrei sind. Es gibt keine magnetischen Ladungen und keine magnetischen Monopole. Magnetische Feldlinien sind entweder in sich geschlossen oder sie winden sich unendlich, ohne in sich zurückzulaufen. Der magnetische Fluss durch jede geschlossene Hüllfläche wird zu Null.
2. Maxwellgleichung in Differentialform im statischen Feld
\(\nabla \cdot \overrightarrow B = div\overrightarrow B = 0\)
2. Maxwellgleichung in Differentialform im zeitlich veränderlichen Feld
\(\nabla \cdot \overrightarrow B = div\overrightarrow B = 0\)
2. Maxwellgleichung in Integralform
\(\oint\limits_A {\overrightarrow B } \,\,d\overrightarrow A = 0\)
3. Maxwellgleichung
Das Faradaysches Induktionsgesetz
\( - \int\limits_A {\dfrac{{\partial \overrightarrow B }}{{\partial t}}} \,d\overrightarrow A + \int\limits_1^2 {\left( {\overrightarrow v \times \overrightarrow B } \right)} \,\,ds = - \dfrac{{d\Phi }}{{dt}}\)
besagt, dass jede Änderung des magnetischen Flusses \(\Phi \) durch eine verkettete Leiterschleife, egal ob diese durch die Bewegung einer Spule im Magnetfeld (Bewegungsinduktion) oder zufolge einer zeitlichen Änderung des Magnetfeldes (Ruheinduktion) verursacht ist, eine elektromotorische Kraft (EMK) bewirkt, und somit eine Urspannung induziert.
3. Maxwellgleichung in Differentialform im statischen Feld
\(\nabla \times \overrightarrow E = rot\overrightarrow E = 0\)
3. Maxwellgleichung in Differentialform im zeitlich veränderlichen Feld
\(\nabla \times \overrightarrow E = rot\overrightarrow E = - \dfrac{{\partial \overrightarrow B }}{{\partial t}}\)
3. Maxwellgleichung in Integralform
\(\oint\limits_s {\overrightarrow E \,\,d\overrightarrow s } = - \int\limits_A {\dfrac{{d\overrightarrow B }}{{dt}}} \,\,d\overrightarrow A \)
4. Maxwellgleichung
Der Durchflutungssatz
\(\Theta = \oint\limits_s {\overrightarrow H } \,\,d\overrightarrow s = \int\limits_A {\overrightarrow S \,\,d\overrightarrow A } = \sum\limits_k {{I_k}} = {U_m}\)
beschreibt den Zusammenhang zwischen der magnetischen Durchflutung Theta und dem verursachenden Strom S. Er besagt, dass geschlossene magnetische Feldlinien von einem Strom durchflossen bzw. „durchflutet“ werden, bzw. umgekehrt formuliert, dass ein elektrischer Strom von geschlossenen magnetischen Feldlinien umgeben ist.
Das Amperesche Durchflutungsgesetz mit dem Maxwell-Ergänzungsterm besagt, dass die magnetische Feldstärke proportional zur elektrischen Stromdichte und der Änderung des elektrischen Feldes ist.
4. Maxwellgleichung in Differentialform im statischen Feld
\(\nabla \times \overrightarrow H = rot\overrightarrow H = \overrightarrow {{S_L}} \)
4. Maxwellgleichung in Differentialform im zeitlich veränderlichen Feld
\(\nabla \times \overrightarrow H = rot\overrightarrow H = \overrightarrow {{S_L}} + \dfrac{{\partial \overrightarrow D }}{{\partial t}}\)
4. Maxwellgleichung in Integralform
\(\oint\limits_s {\overrightarrow H } \,\,d\overrightarrow s = \overrightarrow I + \int\limits_A {\dfrac{{d\overrightarrow D }}{{dt}}} \,\,d\overrightarrow A \)
Anmerkung: Die elektrische Stromdichte S wird auch oft mit J bezeichnet. Wir verwenden J aber für die magnetische Polarisation.
Wellengleichung der elektromagnetischen Welle
Veränderliche elektrische und magnetische Felder erzeugen einander gegenseitig. Die Lösungen der nachfolgend beschriebenen Wellengleichung für das elektrische und das magnetische Feld beschreiben die Ausbreitung von elektromagnetischen Feldern als Wellen mit Lichtgeschwindigkeit im Vakuum. Aus diesen Wellengleichungen ist die Kopplung zwischen E und B im Unterschied zu den Maxwell Gleichungen jedoch nicht mehr ersichtlich.
\(\eqalign{ & \dfrac{{{\partial ^2}\overrightarrow E }}{{\partial {t^2}}} = {c^2} \cdot \Delta \overrightarrow E = \dfrac{1}{{{\mu _0}{\varepsilon _0}}} \cdot \Delta \overrightarrow E \cr & \dfrac{{{\partial ^2}\overrightarrow B }}{{\partial {t^2}}} = {c^2} \cdot \Delta \overrightarrow B = \dfrac{1}{{{\mu _0}{\varepsilon _0}}} \cdot \Delta \overrightarrow B \cr} \)
Bedeutung der Maxwell-Gleichungen geht über die Elektrodynamik hinaus
Die elektromagnetische Wechselwirkung ist neben der Gravitation sowie der starken- bzw. schwachen Wechselwirkung eine der 4 fundamentalen Wechselwirkungen der Physik.
Ursprünglich waren die elektrische und die magnetische Wechselwirkung getrennt, doch mit den 4 Maxwell Gleichungen gelang es, diese beiden Wechselwirkungen zur elektromagnetischen Wechselwirkung zusammen zu fassen.
Maxwell beschrieb wie elektrische und magnetische Felder durch Ladungen und Ströme erzeugt werden und wie sie sich bei zeitlicher Veränderung gegenseitig bedingen.
Dies führte zunächst
- 1873 zu einer Vereinheitlichung elektrischer und magnetischer Phänomene,
- zur Vorhersage der elektromagnetischen Welle durch Hertz 1886, weiters
- zur Herleitung der speziellen Relativitätstheorie 1905 durch Einstein, weiters
- 1940 zur Quantenelektrodynamik und durch
- Einbeziehung der schwachen Wechselwirkung 1964 zur elektroschwachen Wechselwirkung.
Indem auch noch die starke Wechselwirkung eingebunden wurde, entstand das Standardmodell der Teilchenphysik, welches seit der Entdeckung des Higgs-Bosons 2012 als abgeschlossen gilt.
Sollte es zukünftig gelingen auch noch die Gravitation und somit die Allgemeine Relativitätstheorie mit einzubeziehen, hätte man alle 4 fundamentalen Wechselwirkungen in einer Quantengravitationstheorie vereint. Die heute vielversprechendsten Ansätze dafür sind die Supersymmetrie und die Stringtheorie.