Aufgabe 3052

1. Teilaufgabe:

Da die Geschwindigkeit von Bettina als Funktion v(t) beschrieben wird, können wir die Strecke, die sie in einer bestimmten Zeit zurücklegt, durch das Integral ihrer Geschwindigkeit über diese Zeit berechnen.

Wir lösen das bestimmte Integral 

\(\eqalign{ & v\left( t \right) = - 0,08 \cdot {t^2} + 16 \cr & \int\limits_o^{{t_1}} {v\left( t \right)} \,\,dt = 10 \cr & \int\limits_o^{{t_1}} {\left( { - 0,08 \cdot {t^2} + 16} \right)} \,\,dt = 10 \cr} \)

mit Hilfe von Technologie:

Geogebra

• Wir geben im CAS Teil die Gleichung v(t) ein
• Schreiben das Integral an, dessen obere Grenze wir berechnet haben wollen
• Wir "lösen numerisch" die Aufgabenstellung

Bild

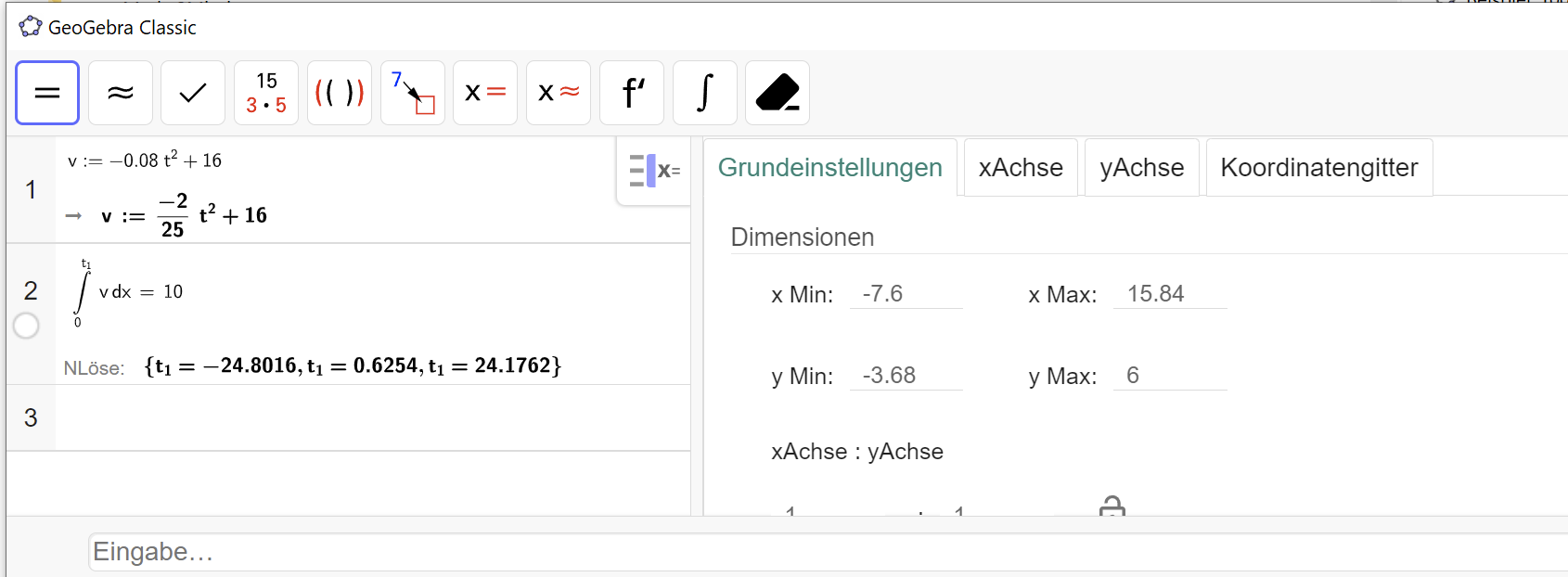
Wir erhalten die 3 Lösungen einer Gleichung 3. Grades:

\(\eqalign{ & 0 \leqslant t \leqslant 2 \cr & \left( {{t_{1,1}} \approx - 24,80} \right) \cr & {t_{1,2}} \approx 0,625408 \cr & \left( {{t_{1,3}} \approx 24,1762} \right) \cr} \)

→ Bettina benötigt für die ersten 10 km rund 0,6 h.

Etwas altmodischer, aber letztlich auch mit Technologie:

Das bestimmte Integral über v(t) lässt sich noch einfach "mit der Hand" berechnen. Die Gleichung 3. Grades müssen wir dann ebenfalls mittels Technologieeinsatz wie folgt lösen:

\(\eqalign{ & v\left( t \right) = - 0,08 \cdot {t^2} + 16 \cr & \int\limits_o^{{t_1}} {v\left( t \right)} \,\,dt = 10 \cr & \int\limits_o^{{t_1}} {\left( { - 0,08 \cdot {t^2} + 16} \right)} \,\,dt = 10 \cr & - 0,08 \cdot \int\limits_0^{{t_1}} {{t^2}\,\,dt + 16 \cdot } \int\limits_0^{{t_1}} {dt} = 10 \cr & \left[ { - 0,08 \cdot \dfrac{{{t^3}}}{3} + 16 \cdot t} \right]_0^{{t_1}} = 10 \cr & \left( { - 0,08 \cdot \dfrac{{{t_1}^3}}{3} - 0} \right) + \left( {16 \cdot {t_3} - 0} \right) = 10 \cr & - \dfrac{{0,08}}{3} \cdot {t_1}^3 + 16 \cdot t = 10 \cr & \cr & 0 \leqslant t \leqslant 2 \cr & \left( {{t_{1,1}} \approx - 24,80} \right) \cr & {t_{1,2}} \approx 0,625408 \cr & \left( {{t_{1,3}} \approx 24,1762} \right) \cr} \)

→ Bettina benötigt für die ersten 10 km rund 0,6 h.

2. Teilaufgabe:

Die Beschleunigung a(t) ergibt sich aus der 1. Ableitung der Geschwindigkeit v(t) nach der Zeit. Die 1. Ableitung v'(t) lässt sich einfach "mit der Hand" berechnen. Dann berechnen wir den Wert der Beschleunigung zum Zeitpunkt t=1

\(\eqalign{ & v\left( t \right) = - 0,08 \cdot {t^2} + 16 \cr & a\left( t \right) = v'\left( t \right) = - 0,08 \cdot 2 \cdot t = - 0,16 \cdot t \cr & \cr & a\left( {t = 1} \right)v'\left( {t = 1} \right) = - 0,16 \cr} \)

→ Die Beschleunigung zum Zeitpunkt t = 1 beträgt –0,16 km/h².

Nachfolgendes Video des BMBWF, welches in den Lösungsweg dieser Aufgabe eingebettet ist, um ein breites Spektrum an Informationen anzubieten, wird auf Grund von Privatsphären-Einstellungen nicht automatisch geladen.

Initiieren Sie das Laden des Videos, werden womöglich personenbezogene Daten in die USA zur Nutzeranalyse durch YouTube übermittelt. Datenschutzbestimmungen von YouTube